Lecture 24: Pointer and shape analysis
Always active area of research.
We could say: “every analysis grows until it incorporates a pointer analysis”.
Introduction
Pointers and references: a way to manipulate values through a level of indirection.
Uses:
- dynamically allocated data structures
- parameter passing by value and reference
- in compiled code, e.g. left-hand side of assignment evaluates to a memory address
Different programming languages have different variations.
Classification by memory safety:
- memory unsafe
- pointers - in C, C++, assembly
- essentially like addresses, can be incremented
- problems with buffer overruns, dangling pointers, memory leaks - major cause of critical flaws in OS, a big failure of C memory model that manifested decades after its invention
- references
- in ML, ocaml, Java, Scala
- can only redirect and follow a reference, cannot increment like a numerical address
- used with garbage collection
- no dangling pointers, fewer memory leaks, type safety
We mostly look at references, but that also applies to C (but there more work may be needed to be sound).
Examples
#include <stdio.h> int main() { int x; int* p; p = &x; x = 3; *p = 4; if(x==3) { printf("3\n"); } else { printf("not 3\n"); } }
Some of the questions we may want to answer include:
- Can compiler prove one branch is dead?
- Can it do common subexpression elimination?
x = sin(z); *p = 4.0; y = x + sin(z);
Here we cannot be sure of the value of x after the assignment to *p, because p might point to x. So we would be interested if finding out whether we can reuse the computation of complex expression sin(z).
Another question we might be interested in answering:
Is
int* p1, p2; ...S... *p1 = E1; *p2 = E2;
equivalent to
int* p1, p2; ...S... *p2 = E2; *p1 = E1;
There are also corresponding examples in Java, ocaml.
x.f = 3; p.f = 4; if(x.f==3) { printf("3\n"); } else { printf("not 3\n"); }
let x = ref 3 in let p = x in p := 4; if((!x)=3) then print_string("3\n") else print_string("not 3\n")
How we can describe this semantically? (Recall verification condition generation in the presence of structures): we can view functions as arrays:
f[x] = 3; f[p] = 4; if(f[x]==3) { printf("3\n"); } else { printf("not 3\n"); }
In C and ML references, there is an implicit 'cell content' field.
x.f = y
becomes
f := f(x:=y)
Expanding function update:
f(x:=y)(z) = IF(z=x,y,f(z))
Key question for reasoning about the result of such IF expressions: do two pointers (references) point to same location, are two 'memory array' indices equal.
To try answer these questions, we use the following techniques:
- pointer analysis: represent (usually disjoint) sets of locations to which each variable points to. For example, if we can determine that a pointer p points to an abstract location 1, and q points to location 2. If location 1 and location 2 are disjoint, then we can be sure that p and q do not overlap.
- alias analysis: can two symbolic expressions be an 'alias' for the same physical location i.e. can they point to the same location.
The following sections outline some simple approaches taken to perform these kinds of analyses.
Unique references
The idea here is to check if a variable is the only way to access a location.
In C, we can perform an “address taken” check:
- if there is no &x expression in C code anywhere, then x is not aliased
In languages like Java, we can do the following to ensure references are unique:
- restrict operations so that there is at most one pointer to a given object after every operation
- disallow x=y where x,y are references
- instead, allow only statements that maintain the uniqueness invariant:
x = new C();
x = y--;
same as: x=y; y=null;
x = y.f--;
same as: x=y.f; y.f=null;
p(y--);
same as: t=y; y=null; p(t); - for fresh var t
Relaxation: allow x=y assignment if y is not live afterwards (adding y=null would then have no effect, so we can omit it).
Binary search tree traversal:
while (n != null && n.data != x) { if (x < n.data) { n = n.left; } else { n = n.right; } }
using unique pointers?
while (n != null && n.data != x) { if (x < n.data) { n = n.left--; // ? } else { n = n.right--; // ? } }
Linear types and linear logic The idea of linear types is to not allow something to be used multiple times.
- introduce a type system that tracks resources (e.g. references)
- basic approach: assumptions are multisets (elements can repeat), cannot use one assumption twice in a proof
What is the invariant that unique reference systems ensure? In every state, the location has at most one incoming edge.

where
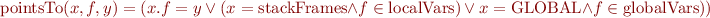
Recent references
Ownership types
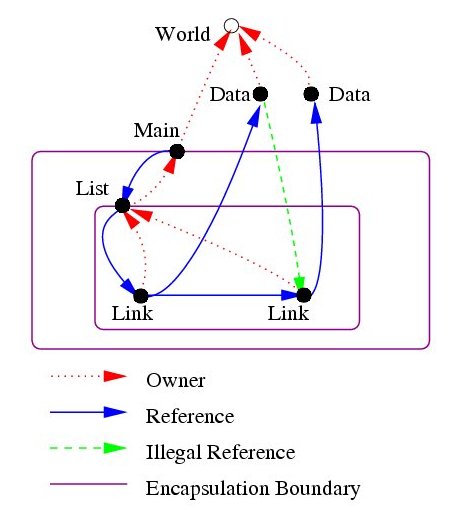
A summary to introduce ownership types from reference 1 (link below): “Ownership types impose structural restrictions on object graphs based on statically definable and checkable notions of owner and representation. The owner of an object is another object and its representation is the objects owned by it. Ultimately, ownership types enforce a statically-checkable notion of encapsulation: every object can have its own private collection of representation objects which are not accessible outside the object which owns them.”
Why private fields are not sufficient (explanation in reference 2): In Java, if a field is declared to be private to a class, it cannot be accessed outside the class using that field name. However, Java allows the contents of a private field to be returned by a method. Using ownership types, this is not allowed, so we have object protection, which stronger that the name protection offered by normal programming languages.
Typical kind of a property enforced: the indicated edge is an articulation edge in a graph: if a node is reachable from a root, it must be reachable through a given edge.
Identify owners statically by some references that are immutable in a given scope
- 'this' always points to same thing within a method
- final references of 'this' and final local variables
Along with standard types, also track owner of objects, e.g.
- allow references from owner to its owned objects
- allow references between objects with same owner
- disallow other references
This diagram and the code that goes along with it are more fully explained in reference 1.
References
Steensgard's analysis
A nonstandard type system: each type describes a set of locations (static, stack, and dynamically allocated).
- flow insensitive
- interprocedural
- almost linear - unification based
Example: x has type 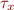 and y has type
and y has type 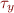 . If there is a statement x=y and y can store a pointer, then types of x and y are unified i.e.
. If there is a statement x=y and y can store a pointer, then types of x and y are unified i.e. 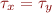
Unification:
Start optimistically by saying all variables have distinct types, and then merge types when there is an assignment. In other words, we are computing the smallest equivalence relation. For this purpose, we can use a union-find data structure (inverted trees) to represent equivalence classes.
This type of analysis is efficient.
References
Andersen's analysis
Here, when there is an assignment of the form x=y, we say that the type of y is a subset of the type of x i.e. 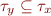 which is the same as
which is the same as 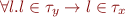 .
.
Context is program specialization: given program 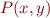 and a known input
and a known input  , generate a specialized, more efficient, program
, generate a specialized, more efficient, program 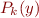 such that
such that 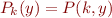 .
.
Run-time specialization: convert 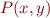 into program that takes
into program that takes  , then produces
, then produces 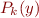 .
.  is determined at run-time, and you can create the copy of
is determined at run-time, and you can create the copy of 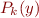 you need.
you need.
Needed a series of analyses, but most known for its pointer analysis.
- context sensitive
- subset based (as opposed to unification-based)
References
Example analysis
Set constraints for flow-insensitive, subset-based analysis, field-sensitive allocation-site based model.
Set for each local and global reference variable and each field.
Elements of sets are labels  denoting objects allocated at program point
denoting objects allocated at program point  .
.
Example:
We can define the set 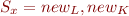 which means that the local variable x can point to objects allocated at program point
which means that the local variable x can point to objects allocated at program point  or
or  . If we also say that
. If we also say that 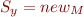 , then we know that x and y cannot point to the same object.
, then we know that x and y cannot point to the same object.
Example assignments:
(Easy to remember rule: 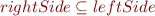 )
)
L: x=new C();
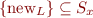
x=y
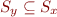
x.f=y
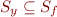
L: x=y.f

Here x and y are not distinct because we do not distinguish between x.f and y.f. Therefore we would like to make the analysis more precise:
Example 2: can we prove that after
x = new C(); y = x; x.f = new C(); y.f = new C(); x1 = x.f; y1 = y.f;
x1 and y1 are the same?
Here we will create a set for each local and global reference variable, as well as for a pair of variable and field:
L: x=new C();
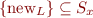
x=y
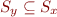
x.f=y
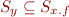
L: x=y.f

This defines everything that can point to the same thing as y.
Now for the last two assignments in example 2 we would have:
x1 = x.f;
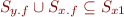
y1 = y.f;
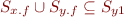
Which shows that x1 and y1 are not distinct.
An important limitation of this technique (which also applies to specifying set constraints) is that each variable has to be considered individually.
Context-sensitive interprocedural pointer analyses:
Shape Analysis
This is a quick example to illustrate the idea of shape analysis. Consider the following statements:
x=y.f.g
x==y
We want to know whether the second statement is true. This depends on the shape of the structure on the heap. If it is a tree, then x and 'y may not point to the same object, so the statment does not not hold. If it is a structure that allows cycles, then the statement could be true.
So you perform shape analysis to “determine 'shape invariants' for programs that perform destructive updating on dynamically allocated storage” (ref: Parametric shape analysis via 3-valued logic).
Analyses with graph-based models of memory
This summary was compiled from the lecture notes and from reference 1 below (where the graph, its construction and other details are explained much more precisely).
The idea here is to represent the state of the memory after some statement in the program by building a graph. A node in the graph represents either
- a simple variable (then called a variable node) or
- a set of heap nodes
 (recall from preivous section that
(recall from preivous section that  is the set of all objects allocated on the heap at program point
is the set of all objects allocated on the heap at program point  )
)
Variable nodes and fields of heap nodes model locations in run-time data structures where pointers may be stored.
Edges in the graph represent pointer values. Edges originate either from variable nodes or from fields within heap nodes and are directed towards heap nodes. (Note: variable nodes do not contain fields, therefore edges cannot be directed towards variable nodes).
The graph contains a finite number of nodes if we build one abstract location  per allocation site
per allocation site  . This allocation site model was the one presented in class, although there could be other methods for merging heap nodes in the graph.
. This allocation site model was the one presented in class, although there could be other methods for merging heap nodes in the graph.
Loops represent the unbounded size of a data structure.
Assignments
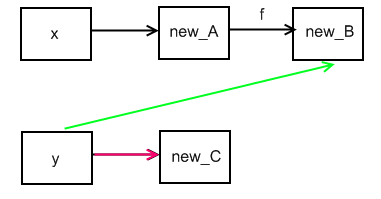
We consider assignments of the form y = x.f or x.f = y. These change the graph in the following way:
y = x.f
Add an edge directed from the variable node for y to the set of nodes reached by leaving fields in x (or the set of nodes that x belongs to). This is the green edge in the diagram below. Remove the old outgoing edge of y (the red edge in the diagram below). This is called a strong update because we are replacing the old edge with a new edge. If we added the new edge without removing the old one, then we would be performing a weak update.
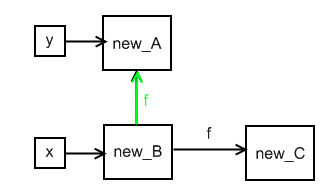
x.f = y
Add an edge from fields in the set of x to the set of nodes that y points to. This is the green edge in the diagram below. This is a weak update since we do not remove old edges leaving the fields of the nodes in x (or the set of nodes, denoted 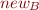 , which includes the object that x points to). If we were sure that
, which includes the object that x points to). If we were sure that 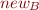 contains a single heap node (and thus that the variable node x points to a single object), then we could remove the old edge, and have a strong update.
contains a single heap node (and thus that the variable node x points to a single object), then we could remove the old edge, and have a strong update.
We want to do strong updates as much as possible because they are the ones that give us more information about what is going on in the memory (who is pointing to who). Therefore we could split abtract locations into smaller sets if they enable us to do a strong update, and then can merge them later if possible.
References
Parameteric analyses
Most of the information below is summarized from reference 1 and the lecture notes I took.
In the shape analysis algorithms we have considered so far, the set of possible memory states (“stores”) that can arise at a given program point are represented by shape graphs, where heap cells are the nodes and sets of indistinguishable heap cells are represented using a single node (often referred to as the summary node) [ref 1]. We have looked at defining indistinguishable heap cells using allocation sites. Reference 1 describes another approach using predicates. They describe a parametric framework for shape analysis. The framework can be instantiated in different ways to create shape analysis algorithms of varying precision.
A parametric framework must address the following issues:
- What is the language for specifying
- the properties of stores that are to be tracked, and
- how such properties are affected by the execution of the different kinds of statements in the programming language?
- How is a shape-analysis algorithm generated from such a specification?
In the paper, to address issue 1, they make use of 2-valued and 3-valued logic:
- 2-valued structures are used to represent concrete stores
- 3-valued structures are used to represent abstract stores
In other words, unary and binary predicates are used to represent the content of variables and pointer-valued structure fields.
First-order formulas with transitive closure are used to specify properties such as
- sharing
- cyclicity
- reachability, etc.
Formulas are also used to specify how the store is affected by the execution of the different kinds of statements in the programming language.
The predicates are parameters to the framework. The specified set of predicates determines the set of data-structure properties that can be tracked, and consequently what properties of stores can be “discovered” to hold at the different points in the program.
To address issue 2, the authors of the paper use an abstract interpretation for the analysis algorithm. The algorithm finds the least fixed point of a set of equations that are generated from the analysis specification.
Applicability
The set of problems that this analysis can be applied to is not predefined like it is with some other shape analysis algorithms (which are only applicable to programs that manipulate structures such as lists, trees, etc).
Characterizing a data structure
Section 2.1 from ref 1 explains:
Each data structure can be characterized by a set of properties such as:
- anchor pointer variables, that is, information about which pointer variables point into the data structure;
- the types of the data-structure elements, and in particular, which fields hold pointers;
- connectivity properties, such as
- whether all elements of the data structure are reachable from a root pointer variable,
- whether any data-structure elements are shared,
- whether there are cycles in the data structure, and
- whether an element v pointed to by a “forward” pointer of another element v
- other properties, for instance, whether an element of an ordered list is in the correct position.
1 and 2 are called core properties because most analyses track them using a pair functions often called the environment and the store.
Connectivity and other properties, such as those mentioned in 3 and 4, are usually not explicitly part of the semantics of pointers in a language, but instead are properties derived from this core semantics. They are essential ingredients in program verification, however, as well as in our approach to shape analysis of programs. Noncore properties are called instrumentation properties.
Representing stores using 2-valued and 3-valued logical structures
A store is represented as a logical structure. A logical structure has a number of individuals and a set of predicates. In a 2-valued logical structure, the predicated map each individual to the value 0 (false) or 1 (true). In a 3-valued logical structure, the predicated map each individual to the value 0 (false), 1/2 (unknown) or 1 (true).
2-valued logical strucures are used to encode concrete stores as follows:
- Individuals represent memory locations in the heap
- pointers from the stack into the heap are represented by unary “pointed-to-by-variable-q” predicates
- and pointer-valued fields of data structures are represented by binary predicates
3-valued logical structures are used to encode abstract stores (like the summary nodes of other algorithms). A 3-valued logical structure corresponds to a set of 2-valued logical structures. The way you abstract a 2-valued logical structure to a 3-valued one is the following: there is some predicates called abstraction predicates. Equivalence classes are formed by individuals in a 2-valued logical structure which have the same values for their abstraction predicates. All members of such equivalence classes are mapped to the same individual in the 3-valued structure. Then, for each nonabstraction predicate in the 2-valued structure, the following value is given to the corresponding predicate in the 3-valued strcture:
- if the predicate has value 0 for all of the individuals in the equivalence class, then its value in the 3-valued structure is 0 (property is false)
- if the predicate has value 1 for all of the individuals in the equivalence class, then its value in the 3-valued structure is 1 (property is true)
- if the predicate has value 0 for some of the individuals and 1 for others in the equivalence class, then its value in the 3-valued structure is 1/2 (don't know whether property holds or not)
This concludes the summary of the first 10 pages of reference 1 below, and should help you understand what was covered in class. The paper explains everything in more detail and continues for another ~70 pages, so there is plenty more details if you are interested.
Reasoning about predicates using decision procedures
Reference 3 below introduces Bohne, an algorithm for inferring loop invariants of programs that manipulate heap-allocated data structures. It also takes properties to be verified as parameters. What makes it unique is the use of a precise abstraction domain that can express detailed properties of a program's infinite memory, and a range of techniques for exploring this analysis domain using decision procedures. The algorithm also uses predicates to partition sets of objects, which is useful for analyzing shape properties (e.g. transitive closure) and also for combining shape properties with sorting properties and properties expressable using linear arithmetic and first-order logic.
The symbolic shape analysis algorithm relies on decision procedures for expressive logics to perform synthesis of loop invariants. The system then verifies that the synthesized invariants are sufficient to prove the absence of errors and to prove the postcondition. During the invariant synthesis, the analysis primarily uses the MONA decision procedure with field constraint analysis to reason about expressive invariants involving reachability in tree-like linked structures.
Bohne has been deployed in the verification systems Hob and Jahob.
References
- Pointer Assertion Logic Enginer - verification condition generation, MSOL over strings - no loop invariant inference
- Verifying Complex Properties using Symbolic Shape Analysis - loop invariant inference, wider class of structures
Separation logic
In reference 2 below, Reynolds introduces separation logic, which is an extension of Hoare logic which permits reasoning about programs with mutable shared data structures. Assertions are extended using a separation conjuction that asserts that its subformulas hold for disjoint parts of the heap, and a closely related separating implication. Together with the definition of predicates, this extension permits the concise and flexible description of structures with controlled sharing.
The separating conjunction is a logical operation  that asserts that
that asserts that  and
and  hold for disjoint parts of the heap. i.e. you can split the heap s.t.
hold for disjoint parts of the heap. i.e. you can split the heap s.t.  holds for one portion and
holds for one portion and  for the other. The precise semantics are as follows:
for the other. The precise semantics are as follows:
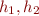 - partial functions from locations to values. i.e. they represent a part of the heap.
- partial functions from locations to values. i.e. they represent a part of the heap.
![Equation \begin{equation*}
[[F_1 * F_2]]h = \exists h_1,h_2. \mbox{disjointDomains}(h_1,h_2)\ \land\ h=h_1\cup h_2\ \land\ [[F_1]]h_1\ \land\ [[F_2]]h_2
\end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/imgcdbd051bdb2bd74fa8900297f171dac7.png)
In English:  is true in a heap
is true in a heap  if there exist two parts of the heap
if there exist two parts of the heap  and
and  such that all of the following are true:
such that all of the following are true:
 and
and  have disjoint domains
have disjoint domains is the union of
is the union of  and
and 
 is true for all locations in
is true for all locations in 
 is true for all locations in
is true for all locations in 
In Hoare logic, you have rules like this {P}S{Q} where  is the formula that must be true before the statement
is the formula that must be true before the statement  executes (the precondition) and
executes (the precondition) and  is the formula that must be true after
is the formula that must be true after  executes (postcondition). So what we want to do here is to infer the frame rule {P*R}S{Q*R} from {P}S{Q}, so that we can make sure that no variable occurring in
executes (postcondition). So what we want to do here is to infer the frame rule {P*R}S{Q*R} from {P}S{Q}, so that we can make sure that no variable occurring in 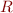 is modified by
is modified by  . This allows you to extend the specification to the variables and parts of the heap that are actually used by
. This allows you to extend the specification to the variables and parts of the heap that are actually used by  (this is referred to as the footprint of
(this is referred to as the footprint of  ). As Reynolds says, the frame rule is the key to “local reasoning” about the heap. Then he quotes another paper (reference 24 in his paper):
). As Reynolds says, the frame rule is the key to “local reasoning” about the heap. Then he quotes another paper (reference 24 in his paper):
“To understand how a program works, it should be possible for reasoning and specification to be confined to the cells that the program actually accesses. The value of any other cell will automatically remain unchanged.”
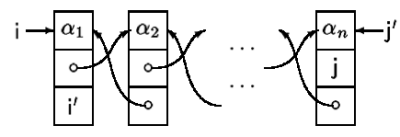
List example
To prove properties about a list, sequences are used as abstract values. In the following example,  and
and  denote sequences, and
denote sequences, and  denotes an empty sequence. To describe the representation of a singly-linked list we write
denotes an empty sequence. To describe the representation of a singly-linked list we write 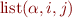 where where there is a list segment from i to j representing the sequence
where where there is a list segment from i to j representing the sequence  .
.
Inductive definitions:
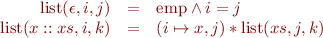
Here a list has been generalized list segments where the separating conjunction is used to prohibit cycles within the list segment.
This is about all we covered in class. On page 10 of Reynold's paper there is an example of a removal from a linked list, when I did not present here since it's easy to follow if you just consult the notations in the paper. For those who are bored by such small examples, there is also a more involved example with the body of a while loop, where the final assertion is the invariant of the while command.
References
Shape analysis with inductive recursion synthesis:
- uses separation logic
- infers inductively defined predicates automatically using inductive recursion synthesis (looks at code that constructs data structure)
- truncation points: tree-like structures with 'holes'
- interprocedural analysis
- infers loop invariants and shapes for recursive procedures
- program slicing reduces the size of analyzed program, based on Steesgaard-like analysis (x.f=y with x,y same type means recursive data structure)
- no user-supplied annotations
Illustrates the depth and achievements of modern shape analysis research.