LARA

Lecture 11

Modular analysis of procedures

Inlining specifications. Last part of SAV07 Homework 4.

Postconditions that refer to values of variables in the precondition.

The meaning of modifies clauses.

ASTREE Static Analyzer

The Octagon Abstract Domain

Link to paper

A Static Analyzer for Large Safety-Critical Software

Link to paper

Section 5.4: A remark on notation:

  • if $\rho$ denotes the state and $S$ is a deterministic statement, then $[\![S]\!]^s(\rho)$ represents the new state after executing the statement; the relation corresponding to statement semantics would be $\{(S,[\![S]\!]^s(\rho)) \mid \rho \mbox{ is a state, mapping variables to their values \}$.
  • this function is extended to map sets of states to sets of states, which gives function mapping $E$ to $[\![S]\!]^c(E)$ and is what we called strongest postcondition $sp(S,E)$.
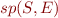  • this is abstracted to abstract domain

Domains used

  • octagons (see above paper)
  • ellipsoid

Widening with tresholds.

Sound approximation of real numbers with floating point calculations.

Improving precision

  • trace partitioning: recover some of the path sensitivity of weakest preconditions
  • decision trees
  • loop unrolling
  • procedures are inlined

Packing: computing relationships between groups of variables and not all variables

  • for octagons
  • for decision trees

Results

  • the absence of false alarms is remarkable, result of heavy tuning of the analysis to given progrma
  • main loop invariant is 4.5MB

Combination of Abstractions in the ASTRÉE Static Analyzer

Note Section 4.1 on how many of the standard assumptions of the domain do not hold any more for such a complex analyzer.

Consider Example 3 of non-monotonicity in the presence of widening. The reason that the result is less precise starting from [0,0] interval for y instead of [0,9] is because widening to [0,$+\infty$] is applied before the fixepoint interval [0,9] is reached.

Section 5 deals with communicating information between different domains. The functions that are defined are mostly various form of approximating conjunction (intersection of sets of states). There are many such functions because arguments and results can belong to different domains.