This is an old revision of the document!
Forward and backward propagation
Let  denote the result of propagating backward the error conditions, that is, the negation of postcondition. We define
denote the result of propagating backward the error conditions, that is, the negation of postcondition. We define 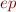 by
by
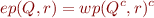
for all  . Here for any set of states
. Here for any set of states  we write
we write  for the complement of
for the complement of  , that is, the set
, that is, the set 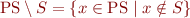 .
.
If 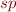 is the postcondition operator, that is,
is the postcondition operator, that is,
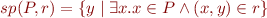
1. Then show that

where 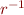 denotes the inverse of relation
denotes the inverse of relation  . In other words, computing weakest preconditions corresponds to propagating possible errors backwards.
. In other words, computing weakest preconditions corresponds to propagating possible errors backwards.
Galois Connection
In the lecture we talked about a special case of Galois connection, called Galois insertion. Galois connection is in general defined by two monotonic functions  and
and 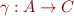 between partial orders
between partial orders  on
on  and
and  on
on  , such that
, such that

for all  and
and  .
.
2. Show that the condition  is equivalent to the conjunction of these two conditions:
is equivalent to the conjunction of these two conditions:
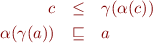
hold for all  and
and  .
.
3. Let  and
and  satisfy the condition of Galois connection. Show that the following three conditions are equivalent:
satisfy the condition of Galois connection. Show that the following three conditions are equivalent:
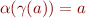 for all
for all 
 is a surjective function
is a surjective function is an injective function
is an injective function
4. State the condition for 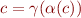 to hold for all
to hold for all  . When
. When  is the set of concrete states and
is the set of concrete states and  is a domain of static analysis, is it more reasonable to expect that
is a domain of static analysis, is it more reasonable to expect that 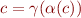 or
or 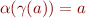 to be satisfied, and why?
to be satisfied, and why?