This is an old revision of the document!
(Draft only!)
Forward and backward propagation
Let  denote the result of propagating backward the error conditions, that is, the negation of postcondition. We define
denote the result of propagating backward the error conditions, that is, the negation of postcondition. We define 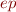 by
by
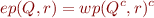
for all  . Here for any set of states
. Here for any set of states  we write
we write  for the complement of
for the complement of  , that is, the set
, that is, the set 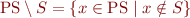 .
.
If 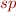 is the postcondition operator, that is,
is the postcondition operator, that is,
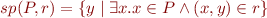
1. Then show that

where 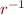 denotes the inverse of relation
denotes the inverse of relation  . In other words, computing weakest preconditions corresponds to propagating possible errors backwards.
. In other words, computing weakest preconditions corresponds to propagating possible errors backwards.
Galois Connection
In the lecture we talked about a special case of Galois connection, called Galois insertion. Galois connection is in general defined by two monotonic functions  and
and 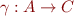 between partial orders
between partial orders  on
on  and
and  on
on  , such that
, such that

for all  and
and  .
.
2. Show that the condition  is equivalent to the conjunction of these two conditions:
is equivalent to the conjunction of these two conditions:
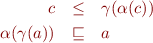
hold for all  and
and  .
.
3. Let  and
and  satisfy the condition of Galois connection. Show that the following three conditions are equivalent:
satisfy the condition of Galois connection. Show that the following three conditions are equivalent:
 for all
for all 
 is a surjective function
is a surjective function is an injective function
is an injective function
Weakest preconditions and relations
Consider a guarded command language with one variable, denoted x, and constructs
assume F assert F havoc(x) c1 [] c2 c1 ; c2
Assume that F can only mention x as the only variable, which takes values from some set  . Program states in our language will be pairs
. Program states in our language will be pairs 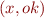 where
where 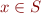 and
and 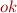 is a boolean value that indicates whether an error has occurred. Therefore, a state is an element of
is a boolean value that indicates whether an error has occurred. Therefore, a state is an element of  .
.
Your task is to define, for each command  , the meaning
, the meaning 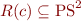 .
.
Using the standard definition of  ,
,

Your goal is to come up with the definition of 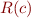 such that wp satisfies the following expected conditions:
such that wp satisfies the following expected conditions:
wp(Q, assume F) = {(x,ok)|F(x) -> (x,ok)∈Q}
wp(Q, assert F) = {(x,ok)|F(x) & (x,ok)∈Q}
wp(Q, havoc(x)) = {(x,ok)|∀x'.(x',ok) ∈ Q}
wp(Q, c1 [] c2) = wp(Q,c1) ∩ wp(Q,c2)
wp(Q, c1 ; c2) = wp(wp(Q,c2),c1)
These conditions correspond to our rules for propagating formulas using wp.
As a hint, you should be able to define
R(c1 [] c2) = R(c1) ∪ R(c2) R(c1 ; c2) = R(c1) o R(c2)
Your remaining task is to define the meaning of assert, assume, and havoc such that all the expected conditions above hold.
Verify your solution by computing
R(assert(false); assume(false))
and
wp(PS, assert(false);assume(false)).
where PS is the set of all program states.