This is an old revision of the document!
Regular expressions
Regular expressions are expressions denoting certain languages. They are precisely those languages that can be built from the singleton languages 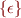 , and
, and  for each
for each  , using operations union (
, using operations union ( ), concatenation (
), concatenation ( ), and iteration (
), and iteration ( ) on languages.
) on languages.
In regular expressions,  is typically denoted
is typically denoted  (sometimes
(sometimes  ), and the curly braces around singleton sets are omitted, so the language
), and the curly braces around singleton sets are omitted, so the language  for
for  is denoted simply
is denoted simply  and the language
and the language 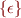 by
by  . The concatenation operator is simply omitted. We next make this more precise. We write
. The concatenation operator is simply omitted. We next make this more precise. We write 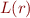 to denote the set that denotes the meaning of a regular expression.
to denote the set that denotes the meaning of a regular expression.
A regular expression over alphabet  is given by:
is given by:
 is a regular expression,
is a regular expression, 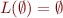
 is a regular expression
is a regular expression 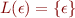
- if
 , then
, then  is a regular expression
is a regular expression 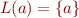
- if
 and
and  are regular expressions, so are
are regular expressions, so are 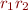 ,
,  , and
, and 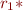 ; we define
; we define 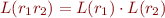 ,
, 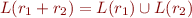 ,
, 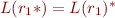
- every regular expression is obtained by a finite number of applications of the rules above.
Example: let 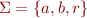 . The regular expression
. The regular expression
(bar)*(a+b)*
denotes the language 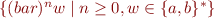 .
.
Example: Integer constants (such as 3123, 9123, 1389123) that do not begin with digit zero are given by (using '|' notation instead of '+'):
(1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)*
Example: let 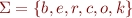
(be*r + coke)*
denotes the set of strings that include:
br, ber, beer, beeer, ... , coke, brcoke, ... , berbrcokecokebeeer
Notes:
- we can introduce shorthand r+ to stand for rr*
- we can allow non-recursive shorthands, for example
posDigit = 1|2|3|4|5|6|7|8|9 digit = 0|posDigit intConst = posDigit digit*