Pure Scala
Description of the Pure Scala subset of Scala, used for specifications in the FunCheck project.
Pure code can be translated into partial functions from inputs to outputs.
Check the status of purity effect system with Lukas.
We will use extraction of pure code for:
- Scala formula language of Vepar
- A version of Funcheck that works only on pure code
Important semantic questions are the status of object allocation and equality.
Abstraction from object graphs to algebraic data types
It seems convenient to introduce abstraction mechanisms that will allow us to define the algebraic data type corresponding to the content of a data structure that has reference equality. We need to think how to do this, but this is for later.
Parametric Polymorphism
And its encoding into Vepar set-theretic type system.
Semantics of Data Structures and Collections
In addition to accessing effect information, Scala mapping should recognize certain special data structures from Scala and map them to mathematical data structures of the specification language. This includes:
Tuples
Scala has one case class per size of tuples, for sizes from 1 to 22 (inclusive).
| Math | Scala |
|---|---|
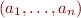 | TupleN(a1, …, aN) (where N ![Math $ \in [1 \ldots 22]$](/w/lib/exe/fetch.php?media=wiki:latex:/imga7c8bcbdab96fa7fb9bdee2028ed210f.png) ) ) |
 | T._k |
Options
The real question is maybe: how do we represent option types in math? Looks like the (almost) simplest possible case of an algebraic data type, except that it's polymorphic.
| Math | Scala |
|---|---|
 | Some(e) |
 | None |
(we should pay attention to the type of each instance of None, though)
Sets
From scala.collection.Set:
| Math | Scala |
|---|---|
 | Set.empty[T] |
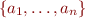 | Set(s : Seq[T]) |
 | A(a) |
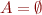 | A.isEmpty |
 | A.equals(B) |
 | A.size |
 | A.subsetOf(B) |
From scala.collection.immutable.Set (which extends scala.collection.Set):
| Math | Scala |
|---|---|
 | A.**(B) or A.intersect(B) |
 | A.++(B) where B : Iterable[T] |
 | A.--(B) where B : Iterable[T] |
 | A.+(a_1, …, a_n) (using varargs) |
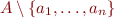 | A.-(a_1, …, a_n) (using varargs) |
 | A.filter(x ⇒ P(x)) (provided  is expressible in Pure Scala) is expressible in Pure Scala) |
Multisets
Multisets are not implemented in the Scala standard library so we have to do it ourselves.
From scala.collection.Multiset:
| Math | Scala |
|---|---|
 | Multiset.empty[T] |
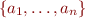 | Multiset(s : Seq[T]) |
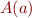 (multiplicity) (multiplicity) | A(a) |
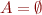 | A.isEmpty |
 | A.equals(B) |
 | A.size |
 | A.subsetOf(B) (which means: 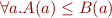 ) ) |
 | A.**(B) or A.intersect(B) |
 | A.++(B) where B : Iterable[T] |
 | A.+++(B) where B : Iterable[T] |
 | A.--(B) where B : Iterable[T] |
 | A.+(a_1, …, a_n) (using varargs) |
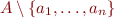 | A.-(a_1, …, a_n) (using varargs) |
 | A.filter(x ⇒ P(x)) (provided  is expressible in Pure Scala) is expressible in Pure Scala) |
Maps
We will see a Map[T1,T2] as a total function from T1 to Option[T2].
| Math | Scala |
|---|---|
 | Map.empty[T1,T2] |
 | (a → b) |
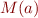 | M.get(a) (returns an Option type) |
 | M.++(N) |
 ( ( is a set of keys) is a set of keys) | M.--(K) |
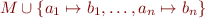 | M.+(a_1 → b_1, …, a_n → b_n) (using varargs) |
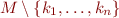 | M.-(k_1, …, k_n) (removes a set of keys) |
Lists
| Math | Scala |
|---|---|
 | Nil |
 | h :: t (which is in fact quite ugly once desugared: t.::(h0), where h0 contains the evaluated version of h to preserve the left-to-right eval. order) |
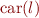 | l.head |
 | l.tail |
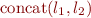 | l_1 ::: l_2 (similar to ::) |
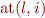 (random access) (random access) | l(i) (returns an Option type) |
Algebraic Data Types
Recognizing algebraic data types is somewhat open ended because of the way they interact with Java-like classes and the fact that they need not be sealed. This can be done in two stages, with the first phase recognizing only those case classes that correspond to ML-style datatype definitions.
Tree hierarchy where leaves are case classes and internal nodes are abstract parameterless sealed classes.