MSOL over Strings

Syntax and Semantics of Weak Monadic Second-Order Logic over Strings

Explanation of the name:

second-order logic: we can quantify not only over elements but also over sets and relations
monadic: we cannot quantify over any relations, just unary relations, that is, sets
over strings: the domain of interpretation are not general graphs, but only strings, so the only built-in relation is a relation that gives us the next position in a string
weak: we consider only finite strings

Alternative name is “monadic second-order logic of one successor”.

Minimalistic syntax for monadic second-order logic is:

$\begin{equation*} F ::= v \subseteq v \mid s(v,v) \mid F \lor F \mid \lnot F \mid \exists v.F \end{equation*}$

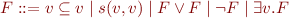
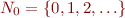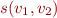As the domain of interpretation we take the set of natural numbers $N_0 = \{0,1,2,\ldots\}$ . We interpret variables as finite subsets of this set, and $\subseteq$ as the subset relation. The relation $s(v_1,v_2)$ is the successor relation on integers lifted to singleton sets.

More precisely, if $e : V \to 2^{N_0}$ then we have the following semantics:

$\begin{eqnarray*} [\![v_1 \subseteq v_2]\!]e &=& (e(v_1) \subseteq e(v_2)) \\ \ [\![s(v_1,v_2)]\!]e &=& (\exists k \in N_0. e(v_1) = \{k\} \land e(v_2)=\{k+1\}) \\ \ [\![F_1 \lor F_2]\!]e &=& [\![F_1]\!]e\ \lor\ [\![F_2]\!]e \\ \ [\![\lnot F]\!]e &=& \lnot ([\![F]\!]e) \\ \ [\![\exists v. F]\!]e &=& \exists S. S\ \mbox{is finite}\ \land\ S \subseteq N_0 \land [\![F]\!](e[v \mapsto S]) \end{eqnarray*}$

What can we express in MSOL over strings

Set operations. The ideas is that quantification over sets with $\subseteq$ gives us the full Boolean algebra of sets.

Two sets are equal: $(S_1 = S_2) = (S_1 \subseteq S_2) \land (S_2 \subseteq S_1)$
Strict subset: $(S_1 \subset S_2) = (S_1 \subseteq S_2) \land \lnot (S_2 \subseteq S_1)$
Set is empty: $(S=\emptyset) = \forall S_1. S \subseteq S_1$
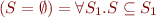
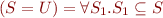
Set is full: $(S=U) = \forall S_1. S_1 \subseteq S$
Set $S$ is singleton (has exactly 1 element): $One(S) = (\lnot (S = \emptyset)) \land (\forall S_1. S_1 \subset S \rightarrow S_1=\emptyset)$
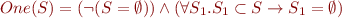
Set membership, treating elements as singletons: $(x \in S) = (x \subseteq S)$
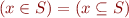
Intersection: $(A = B \cap C) = (A \subseteq B \land A \subseteq C) \land (\forall A_1. A_1 \subseteq B \land A_1 \subseteq C \rightarrow A_1 \subseteq A)$
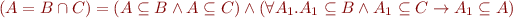
Union: $(A = B \cup C) = (B \subseteq A \land C \subseteq A) \land (\forall A_1. B \subseteq A_1 \land C \subseteq A_1 \rightarrow A \subseteq A_1)$
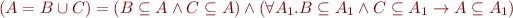
Set difference: $(A = B \setminus C) = (A \cup (B \cap C) = B \land A \cap C = \emptyset)$

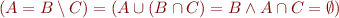
(or just use element-wise definitions with singletons)

If $k$ is a fixed constant, properties $\mbox{card}(A) \geq k$ , $\mbox{card}(A)\leq k$ , $\mbox{card}(A)=k$

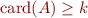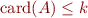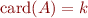
Transitive closure of a relation. If 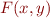$F(x,y)$ is a formula on singletons, we define reflexive transitive closure as follows. Define shorthand

$\begin{equation*} \mbox{Closed}(S,F) = (\forall x,y. One(x) \land One(y) \land x \in S \land F(x,y) \rightarrow y \in S) \end{equation*}$

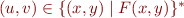Then $(u,v) \in \{(x,y) \mid F(x,y)\}^*$ is defined by

$\begin{equation*} \forall S. u \in S \land \mbox{Closed}(S,F) \rightarrow v \in S \end{equation*}$

Using transitive closure and successors:

Constant zero: $(x=0) = One(x) \land \lnot (\exists y. One(y) \land s(y,x))$
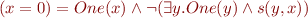
Addition by constant: $(x = y + c) = (\exists y_1,\ldots,y_{c-1}. s(y,y_1) \land s(y_1,y_2) \land \ldots \land s(y_{c-1},x))$
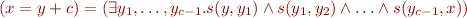
Ordering on positions in the string: $(u \leq v) = ((u,v) \in \{(x,y)|s(x,y))\}^*$
Reachability in $k$ -increments, that is, $\exists k \geq 0. y=x + c\cdot k$ : $\mbox{Reach}_c(u,v) = ((u,v) \in \{(x,y)\mid y=x+c\}^*)$
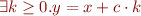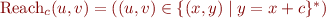
Congruence modulo $c$ : $(x \equiv y)(\mbox{mod}\ c) = \mbox{Reach}_c(x,y) \lor \mbox{Reach}_c(y,x)$

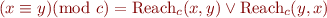
Representing integers. Note that although we interpret elements as sets of integers, we cannot even talk about addition of two arbitrary integers 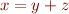$x=y+z$ , only addition with a constant. Also, although we can say 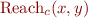$\mbox{Reach}_c(x,y)$ we cannot say in how many steps we reach $y$ from $x$ . However, if we view sets of integers digits of a binary representation of another integer, then we can express much more. 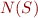If $S$ is a finite set, let $N(S)$ represent the number whose digits are $S$ , that is:

$\begin{equation*} N(S) = \sum_{i \in S} 2^i \end{equation*}$

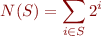
Then we can define addition 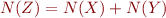$N(Z) = N(X) + N(Y)$ by saying that there exists a set of carry bits $C$ such that the rules for binary addition hold:

$\begin{equation*} \exists C.\ 0 \notin i\ \land \forall i.\ \big(\begin{array}[t]{rcl} ((i \in Z) &\leftrightarrow& ((i \in X) \oplus (i \in Y) \oplus (i \in C))\ \land\\ ((i+1 \in C) &\leftrightarrow& \mbox{atLeastTwo}(i \in X,i \in Y,i \in C)\big) \end{array} \end{equation*}$

where

$\begin{eqnarray*} x \oplus y &=& (x \lor y) \land \lnot (x \land y) \\ \mbox{atLeastTwo}(x,y,z) &=& (x \land y) \lor (x \land z) \lor (y \land z) \end{eqnarray*}$

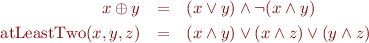
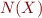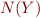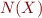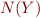This way we can represent entire Presburger arithmetic in MSOL over strings. Moreover, we have more expressive power because $X \subseteq Y$ means that the one bits of $N(X)$ are included in the bits of $N(Y)$ , that is, the bitwise or of $N(X)$ and $N(Y)$ is equal to 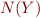$N(Y)$ . In fact, if we add the relation of bit inclusion into Presburger arithmetic, we obtain precisely the expressive power of MSOL when sets are treated as binary representations of integers (Indeed, taking the minimal syntax of MSOL from the beginning, the bit inclusion gives us the subset, whereas the successor relation 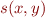$s(x,y)$ is expressible using $y=x+1$ .)