In this lab, we will implement a bounded model-checker (using a SAT solver) and try it on a few examples.

Download and extract the project archive

Run sbt to start the sbt shell, and type run to make sure everything is working properly. The code is filled with holes ??? that you need to fill, with the help of the following instructions.

We define in file TransitionSystem.scala the model we will be using in this lab. These are deterministic finite state machines which maintain boolean variables that can be updated (when receiving inputs) thanks to boolean formulas (given by the transition map). This map should contain an entry for each identifier in stateIds, and each identifier in auxiliaryIds, but no entries for the identifiers in inputIds. See the method next for the precise definition of how the next state is computed (when an input is given). See also the checkWF method to see some well-formedness checks on the transition system. This method is called whenever a transition system is instantiated.

The method dump outputs a dot file and calls the dot executable to transform it into a png file. You need to have dot in your path for this to work. The dot program is part of the Graphviz software.

Alternatively, you can also copy/paste the contents of dot file which is created into this website to get an image.

Your second task is to write an adder for natural numbers represented in binary (unsigned integers). You are given a skeleton code to complete in Adder.scala. The adder maintains an accumulator that sums all the inputs given so far, and a counter to bound the number of inputs. When the counter reaches its maximum capacity, the adder loops on the same state and ignores its inputs. The adder also has an overflow bit to mark when the accumulator overflows.

The adder has three parameters, n for the number of bits of the accumulator, m for the number of bits of the input, and l for the number of bits of the counter. It is required for m to be less than or equal to n.

The sequence accIds contains n boolean variables representing the accumulator, with accIds(0) being the least significant bit. The sequence counterIds contains l boolean variables representing the counter. The m input variables (in inputIds) represent a natural number that we want to add to the state. The n+1 auxiliary variables (in carryIds) are here to hold the values for the carries when doing the addition (of the state plus the input).

Your task is to complete the missing expressions to compute the carries, the accumulator, the counter, and the overflow bit. Look for the TODO comments.

You can debug your adder by interacting with it by running Adder.interactiveTest(6, 4, 2) in the main method (feel free to change the numbers of bits).

You are given in ScalaZ3Interface a function checkSat that checks whether some boolean expression is satisfiable (and returns a satisfying assignment when this is the case). The goal of this exercise is to make use of that function to write a bounded model-checker. Your code will go in checkErrorReachability, which is a method of TransitionSystem. When there exists a path of length k that goes from a state satisfying from to an error state (i.e. a state satisfying the error expression), this function should return it (k+1 states, and k inputs). When returning the path, make sure to refer to the original state variables and not to the fresh intermediary ones.

If this seems too hard at first, you can initially write it for k = 1.

• You should call `checkSat` only once
• You should not use `enumerate` or `next` (these are not useful here)
• You should make use of all the fields that are in the TransitionSystem (stateIds, inputIds, auxiliaryIds, and transition)
• The very first step of your function should be making k + 1 copies of the sequence `stateIds` (for instance by adding an index to the names of the identifiers), k copies of the sequence `inputIds`, and k copies of the sequence `auxiliaryIds`
• When building the expression, you should use `subst` to substitute the original variables that appears in `from`, `error` and `transition(x)` by the copies of you have created.

Run checkNoOverflow(5, 3, 3) and observe that there is an overflow. Run checkNoOverflow(8, 4, 4) and observe that there is no overflow.

• 1. For cases where there are no overflows (such as (8, 4, 4)), explain (in comments) why Adder.invariant is not an inductive invariant. If needed, convince yourself that the invariant is not inductive by running checkInductiveInvariant(invariant, 8, 4, 4).
• 2. Come up with an inductive invariant which implies the no overflow invariant and write it in method inductiveInvariant.
• 3. Check that checkInductiveInvariant(8, 4, 4) prints that your invariant is inductive. Do with the same with other parameters, e.g. 64, 32, 32. Try with checkInductiveInvariant(8, 5, 4) to make sure you get an error.

• The inductive invariant you write must talk about the accumulator, the counter, and the overflow bit. Depending on the number of input bits, think about the mathematical constraint that you want to impose on the counter and the accumulator.
• The inductive invariant need not be a precise description of the reachable states, and can include some non-reachable states.
• The inductive invariant you write only needs to be an inductive invariant for the parameters for which there are no overflows.
• (Typo) It should be l instead of m in val maxSteps: Int = BigInt(2).pow(m).toInt in checkNoOverflow.

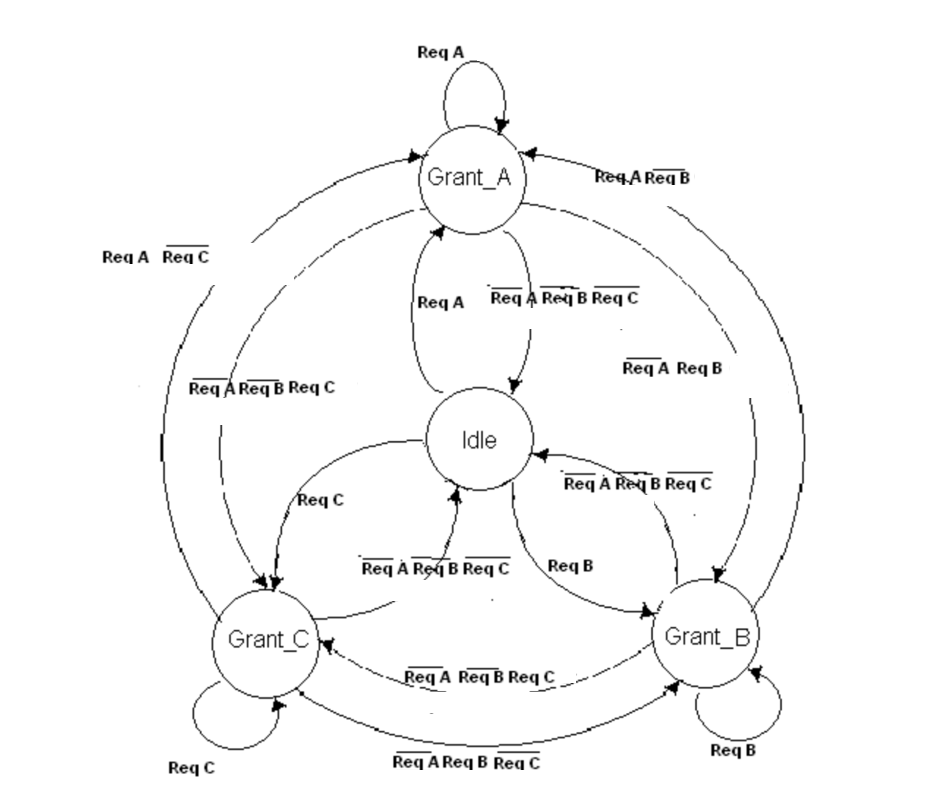
Arbiter.scala describes a system that gives access to some shared resource to components A, B or C, depending on the requests they make. The system should not grant access to the resource to two components at the same time. The state machine diagram below describes the system as it is implemented.

• 1. Write the invariant, stating that exactly one variable out of Idle, GrantA, GrantB, GrantC is true.
• 2. Run the Arbiter.verify() function and observe that the invariant does not hold. There is an input that leads to two (or more) components being granted access to the resource at the same time. Write down the input in the comments.
• 3. By giving priority to A over B and C, and to B over C, fix the system to make sure that the invariant holds. To this end, you only to modify the transition table. Do NOT introduce new state, input, or auxiliary variables in the system.

.