Type Checking Let and Letrec

Let Expressions

Expression

$\begin{equation*} \textbf{let}\ {x:T} = e_1\ \textbf{in}\ e_2 \end{equation*}$

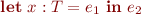
can be viewed as a shorthand for

$\begin{equation*} (\lambda x:T. e_2) e_1 \end{equation*}$

because they both evaluate to $e_2[x:=e_1]$

From this follows the type rule for let expressions:

$\begin{equation*} \frac{\Gamma \vdash e_1:T_1, \ \ \Gamma \oplus \{ x \mapsto T_1 \} \vdash e:T} {\Gamma \vdash (\textbf{let}\ {x:T_1} = e_1\ \textbf{in}\ e) : T} \end{equation*}$

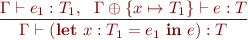
Example: We can represent non-recursive method definitions using let

In this Java-like code

  int f(int x) {
    return x + 3;
  }
  int main(int y) {
    return f(f(y+5));
  }

the main function can be type checked by type checking

  let (f:int->int) = % x:int. x+3 in
    %y:int. f(f(y+5))

Recursive Let (letrec) Expressions

How to represent recursive definitions in lambda calculus? Consider this example

  int g(int x) {
    return (x <= 0 ? 1 : (x+g(x-1)));
  }
  int h(int x) {
    return g(h(x));
  }
  expr

We use recursive version of let, denoted letrec, representing above as

  letrec (g : int->int) = (ite (<= x 0) 1 (+ x (g (- x 1))))
     and (h : int->int) = (g (h x))
  in expr

Type rule for letrec:

$\begin{equation*} \frac{\Gamma \oplus \{ f_1 \mapsto T_1, \ldots, f_n \mapsto T_n \} \vdash e_1:T_1,\ldots,e_n:T_n,e:T} {\Gamma \vdash (\textbf{letrec}\ {(f_1:T_1)} = e_1\, \textbf{and}\, \ldots \textbf{and}\, {(f_n:T_n)} = e_n\ \textbf{in}\ e) : T} \end{equation*}$

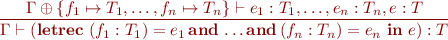
Example: type check the previous code using the letrec rule.

Using Lambda Calculus and Letrec

describes type checking of mutually recursive definitions
result is again expression: supports nested function definitions
- each of $e$ , $e_i$ can contain other letrec expressions