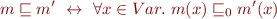Range Analysis

Properties of Interest

A more precise analysis that computes sets to which integer variables belong

For each program point compute interval (or a union of intervals) to which variable belongs

Applications:

Encoding conditions: to check that

assert(e)

never fails, we encode it as

if (!e) {
  ERROR
}

and show that ERROR program point is not reachable

Pointwise lattice - a range for each variable

$\begin{equation*} m \sqsubseteq m' \ \leftrightarrow\ \forall x \in Var.\ m(x) \sqsubseteq_0 m'(x) \end{equation*}$

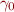$\gamma_0$ for base lattice of variables - given in comments of RangeAnalysisLattice.scala

We lift it to $\gamma$ pointwise, as usual:

$\begin{equation*} \gamma(m) = \{ c : Var \to Int \mid \forall x \in Var.\ c(x) \in \gamma_0(m(x)) \} \end{equation*}$

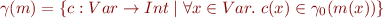
If we view map from variables as a labelled n-tuple, then this is just Cartesian product of 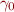$\gamma_0$ of components

NOTE: if 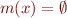$m(x)=\emptyset$ then $\gamma(m)=\emptyset$

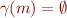
when analysis finishes, if 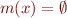$m(x)=\emptyset$ at program point $P$ , then $P$ is unreachable

Monotonicity: by construction

$\begin{equation*} m \sqsubseteq m' \ \rightarrow \gamma(m) \subseteq \gamma(m') \end{equation*}$

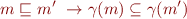
Question: does the converse hold?

Bottom has empty intervals for all variables

Assuming all variables are initially zero, what is the initial abstract element?

By definition – many cases, for each CFG statement and each kind of interval

What is the height of the lattice?

Ensuring termination by widening: