LARA

MiniJava+ Type Rules and Constraints

The type $TUnit$ is used for elements that need to be type-checked but do not carry a type themselves (this includes statements).

Class definitions and subtyping

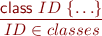
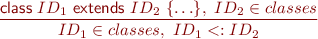
\begin{equation*} \frac{\textsf{class}\ ID\ \{ \ldots \} }{ ID \in classes } \end{equation*}

\begin{equation*} \frac{\textsf{class}\ ID_1\ \textsf{extends}\ ID_2\ \{ \ldots \},\ ID_2 \in classes }{ ID_1 \in classes,\ ID_1 <: ID_2 } \end{equation*}

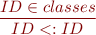
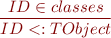
\begin{equation*} \frac{ID \in classes}{ ID <: ID } \end{equation*}

\begin{equation*} \frac{ID \in classes}{ ID <: TObject } \end{equation*}

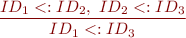
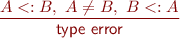
\begin{equation*} \frac{ID_1 <: ID_2,\ ID_2 <: ID_3}{ ID_1 <: ID_3 } \end{equation*}

\begin{equation*} \frac{A <: B,\ A \neq B,\ B <: A} {\textsf{type error}} \end{equation*}

\begin{equation*} TInt <: TInt \end{equation*}

\begin{equation*} TBoolean <: TBoolean \end{equation*}

\begin{equation*} TString <: TString \end{equation*}

\begin{equation*} TIntArray <: TIntArray \end{equation*}

Class variables and methods

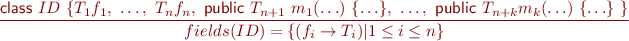
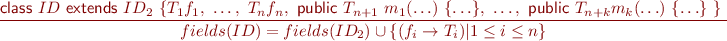
\begin{equation*} \frac{\textsf{class}\ ID\ \{ T_1 f_1,\ \ldots,\ T_n f_n,\ \textsf{public}\ T_{n+1}\ m_1(\ldots)\ \{\ldots\},\ \ldots,\ \textsf{public}\ T_{n+k} m_k(\ldots)\ \{\ldots\}\ \} }{ fields(ID) = \{ (f_i \rightarrow T_i) | 1 \leq i \leq n \} } \end{equation*}

\begin{equation*} \frac{\textsf{class}\ ID\ \textsf{extends}\ ID_2\ \{ T_1 f_1,\ \ldots,\ T_n f_n,\ \textsf{public}\ T_{n+1}\ m_1(\ldots)\ \{\ldots\},\ \ldots,\ \textsf{public}\ T_{n+k} m_k(\ldots)\ \{\ldots\}\ \}\ }{ fields(ID) = fields(ID_2) \cup \{ (f_i \rightarrow T_i) | 1 \leq i \leq n \} } \end{equation*}

\begin{equation*} \frac{\textsf{class}\ ID\ \{ T_1 f_1,\ \ldots,\ T_n f_n,\ \textsf{public}\ T_{n+1}\ m_1(T_1^1,\ \ldots,\ T_1^{l_1})\ \{\ldots\},\ \ldots,\ \textsf{public}\ T_{n+k} m_k(T_k^1,\ \ldots,\ T_k^{l_k})\ \{\ldots\}\ \} }{ methodType(m_j, ID) = (T_j^1 \times \ldots \times \ T_j^{l_j}) \rightarrow T_{n+j}, \forall(1 \leq j \leq k) } \end{equation*}

\begin{equation*} \frac{\textsf{class}\ ID\ \textsf{extends}\ ID_2\ \{ T_1 f_1,\ \ldots,\ T_n f_n,\ \textsf{public}\ T_{n+1}\ m_1(T_1^1,\ \ldots,\ T_1^{l_1})\ \{\ldots\},\ \ldots,\ \textsf{public}\ T_{n+k} m_k(T_k^1,\ \ldots,\ T_k^{l_k})\ \{\ldots\}\ \},\ \forall(1 \leq i \leq k):\ m \neq m_i }{ methodType(m, ID) = methodType(m, ID_2) } \end{equation*}

\begin{equation*} \frac{methodType(m, ID_1) \neq methodType(m, ID_2),\ ID_1 <: ID_2}{\textsf{overriding error}} \end{equation*}

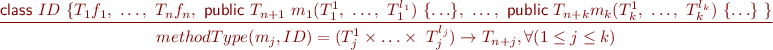
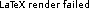
Special main class:

\begin{equation*} \frac{\Gamma \vdash stat : TUnit}{\textsf{class}\ ID\ \{ \textsf{public static void main(String [] args)} \{ stat \} : TUnit } \end{equation*}

Type-checking method bodies

In class $ID$:

\begin{equation*} \frac{\Gamma \oplus fields(ID) \oplus (\textsf{this} \rightarrow ID) \oplus \{ (v_i \rightarrow T_i) | 1 \leq i \leq n \} \vdash stat_1 : TUnit,\ \ldots,\ stat_l : TUnit,\ e : T_S,\ T_S <: T_R } {\Gamma \vdash \textsf{public}\ T_R\ m(T_1 v_1,\ \ldots,\ T_k v_k)\ \{ T_{k+1} v_{k+1};\ \ldots\ T_n v_n;\ stat_1;\ \ldots\ stat_l;\ \textsf{return}\ e; \} : TUnit } \end{equation*}

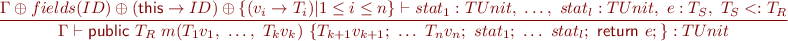
Expressions

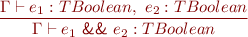
\begin{equation*} \frac{\Gamma \vdash e_1 : TBoolean,\ e_2 : TBoolean}{\Gamma \vdash e_1\ \textsf{\&\&}\ e_2 : TBoolean } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TBoolean,\ e_2 : TBoolean}{\Gamma \vdash e_1\ \textsf{$||$}\ e_2 : TBoolean } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TInt,\ e_2 : TInt}{\Gamma \vdash e_1\ \textsf{+}\ e_2 : TInt } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TString,\ e_2 : TInt}{\Gamma \vdash e_1\ \textsf{+}\ e_2 : TString } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TInt,\ e_2 : TString}{\Gamma \vdash e_1\ \textsf{+}\ e_2 : TString } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TString,\ e_2 : TString}{\Gamma \vdash e_1\ \textsf{+}\ e_2 : TString } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TInt,\ e_2 : TInt}{\Gamma \vdash e_1\ \textsf{-}\ e_2 : TInt } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TInt,\ e_2 : TInt}{\Gamma \vdash e_1\ \textsf{/}\ e_2 : TInt } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TInt,\ e_2 : TInt}{\Gamma \vdash e_1\ <\ e_2 : TBoolean } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TBoolean}{\Gamma \vdash \textsf{!}\ e_1 : TBoolean } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TInt,\ e_2 : TInt}{\Gamma \vdash e_1\ \textsf{==}\ e_2 : TBoolean } \end{equation*}

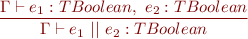
\begin{equation*} \frac{\Gamma \vdash e_1 : TIntArray,\ e_2 : TIntArray}{\Gamma \vdash e_1\ \textsf{==}\ e_2 : TBoolean } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TBoolean,\ e_2 : TBoolean}{\Gamma \vdash e_1\ \textsf{==}\ e_2 : TBoolean } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TString,\ e_2 : TString}{\Gamma \vdash e_1\ \textsf{==}\ e_2 : TBoolean } \end{equation*}

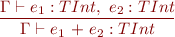
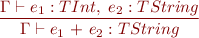
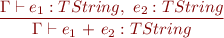
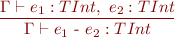
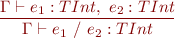
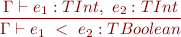
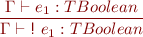
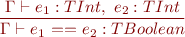
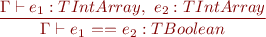
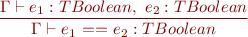
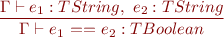
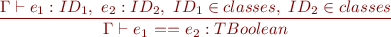
\begin{equation*} \frac{\Gamma \vdash e_1 : ID_1,\ e_2 : ID_2,\ ID_1 \in classes,\ ID_2 \in classes}{\Gamma \vdash e_1\ \textsf{==}\ e_2 : TBoolean } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash e_1 : TIntArray,\ e_2 : TInt}{\Gamma \vdash e_1\textsf{[}e_2\textsf{]} : TInt } \end{equation*}

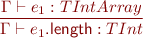
\begin{equation*} \frac{\Gamma \vdash e_1 : TIntArray}{\Gamma \vdash e_1\textsf{.length} : TInt } \end{equation*}

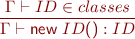
\begin{equation*} \frac{\Gamma \vdash e_1 : TInt}{\Gamma \vdash \textsf{new Int[}e_1\textsf{]} : TIntArray } \end{equation*}

\begin{equation*} \frac{\Gamma \vdash ID \in classes}{\Gamma \vdash \textsf{new }ID\textsf{()} : ID } \end{equation*}

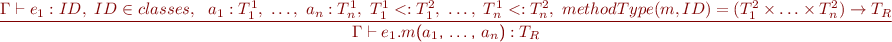
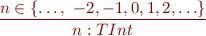
\begin{equation*} \frac{\Gamma \vdash e_1 : ID,\ ID \in classes,\ \ a_1 : T_1^1,\ \ldots,\ a_n : T_n^1,\ T_1^1 <: T_1^2,\ \ldots,\ T_n^1 <: T_n^2,\ methodType(m, ID) = (T_1^2 \times \ldots \times T_n^2) \rightarrow T_R }{\Gamma \vdash e_1\textsf{.}m\textsf{(}a_1\textsf{, \ldots, }a_n\textsf{)} : T_R } \end{equation*}

\begin{equation*} \frac{n \in \{\ldots,\ -2, -1, 0, 1, 2, \ldots\} }{n : TInt} \end{equation*}

\begin{equation*} \frac{}{\textsf{"string constant"} : TString } \end{equation*}

\begin{equation*} \frac{}{\textsf{true} : TBoolean } \end{equation*}

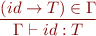
\begin{equation*} \frac{}{\textsf{false} : TBoolean } \end{equation*}

\begin{equation*} \frac{(id \rightarrow T) \in \Gamma }{\Gamma \vdash id : T } \end{equation*}

Statements

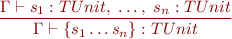
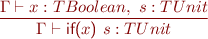
\begin{equation*} \frac{\Gamma \vdash s_1 : TUnit,\ \ldots,\ s_n : TUnit}{\Gamma \vdash \textsf{\{} s_1 \ldots s_n \textsf{\}} : TUnit \end{equation*}

\begin{equation*} \frac{\Gamma \vdash x : TBoolean,\ s : TUnit}{\Gamma \vdash \textsf{if(}x\textsf{)}\ s : TUnit} \end{equation*}

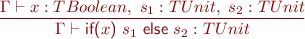
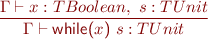
\begin{equation*} \frac{\Gamma \vdash x : TBoolean,\ s_1 : TUnit,\ s_2 : TUnit}{\Gamma \vdash \textsf{if(}x\textsf{)}\ s_1\ \textsf{else}\ s_2 : TUnit} \end{equation*}

\begin{equation*} \frac{\Gamma \vdash x : TBoolean,\ s : TUnit}{\Gamma \vdash \textsf{while(}x\textsf{)}\ s : TUnit} \end{equation*}

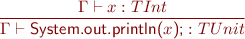
\begin{equation*} \frac{\Gamma \vdash x : TBoolean}{\Gamma \vdash \textsf{System.out.println(}x\textsf{);} : TUnit \end{equation*}

\begin{equation*} \frac{\Gamma \vdash x : TInt}{\Gamma \vdash \textsf{System.out.println(}x\textsf{);} : TUnit \end{equation*}

\begin{equation*} \frac{\Gamma \vdash x : TString}{\Gamma \vdash \textsf{System.out.println(}x\textsf{);} : TUnit \end{equation*}

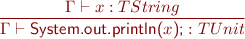
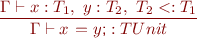
\begin{equation*} \frac{\Gamma \vdash x : T_1,\ y : T_2,\ T_2 <: T_1}{\Gamma \vdash x\ \textsf{=}\ y\textsf{;} : TUnit \end{equation*}

\begin{equation*} \frac{\Gamma \vdash x : TIntArray,\ y : TInt,\ z : TInt}{\Gamma \vdash x\textsf{[}y\textsf{]}\ \textsf{=}\ z\textsf{;} : TUnit \end{equation*}