Live Variable Analysis
For each program point, and each variable approximately compute whether the variable is live at that program point
Definition: a variable  is dynamically live in a concrete program state
is dynamically live in a concrete program state  , if there exists a finite sequence of steps
, if there exists a finite sequence of steps
- starting from

- not containing assignments to
 except as the final statement
except as the final statement - finishing by a statement that reads

Live variable analysis computes for each program point  , for each variable
, for each variable  whether
whether
 is live in every state that reaches program point
is live in every state that reaches program point 
- otherwise: the value of variable may or may not be read in the future - we say that it is live
NOTE: if a static analysis says that the variable is live at program point, we know essentially nothing about it
- but if we know that it is not live, this is useful information
Consider a sequence of instructions:
| code | live variables |
|---|---|
| {z} | |
| x = 42 | |
| {x,z} | |
| y = x + 3 | |
| {x,y,z} | |
| z = y + z | |
| {x} | |
| y = 3 + x | |
| {} |
Applications:
- allocating space for variables (e.g. register allocation for CPU - next lecture)
- if variable not used in future, we can store another variable in the same address
- an alternative to initialization analysis: must be initialized if it will be used
- if variable is used in the future before being assigned, it must be initialized now
- we can do initialization check by checking that no variable is live at CFG entry
Liveness is naturally computed using backwards data-flow analysis
Consider the program execution backwards
- execution is very non-deterministic (e.g. x=3 goes into all values of x)
- mathematically equally well-defined
- introduce an additional state bit to variable, mark it “used” when it is used
- if a state is reached in backward execution where it is used, then it “will be used”
Corresponding backward analysis:
- variable uses flow towards their initializations
- edges in data-flow analysis are interpreted in the opposite way
- analysis starts from the exit point
Final state at the exit point
- no variable is live - no more statements at the end, so no future uses
- this is also the bottom of the lattice
Pointwise Representation
For each variable, store its liveness:
- potentially live (top)
- definitely not live (bottom)
Bottom: map each variable to bottom
Join: pointwise join
- bottom
 top = top
top = top 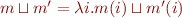
More Elegant Representation
The set of potentially live variables
Bottom: empty set
Join: union
We use this representation
Semilattice for Liveness Analysis
(Semilattice is like lattice but need not have meet.)
Elements are sets  of live variables
of live variables
- we assume no scopes, otherwise use variable descriptions
Join is union
Transfer Functions for Live Variable Analysis
For each statement st in CFG, we introduce sets of variables
- use(st) denote variables used in statement
- def(st) denote variables overwritten in st
For SimpleCFG.scala we have
| st | use(st) | def(st) |
|---|---|---|
| x = y op z | {y,z} | {x} |
| x = y | {y} | {x} |
| Assume[y relOp z] | {y,z} | {} |
| print(y) | {y} |
Examples:
| st | use(st) | def(st) |
|---|---|---|
| x = y + 1 | {y} | {x} |
| x = x + 1 | {x} | {x} |
In ordinary execution, statement
- first uses variables in use(st) to compute some value
- then assigns this value to variables in def(st)
In backward execution, statement
- marks def(st) as not live
- marks use(st) as live
in that order
Transfer function
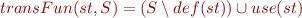
Backwards computation means
- given edge
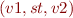 in CFG
in CFG - if
 is the set of variables live at program point
is the set of variables live at program point  , then the contribution to point
, then the contribution to point 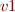 is
is 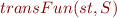
References
- Tiger book, Chapter 10, Chapter 17 (page 358)