Efficiently Emitting Code

Efficiency Problem

Consider concatenation-based implementation

$\begin{equation*} [\![ ((e_1 + e_2) + e_3) + e_4 ]\!] = (([\![e_1]\!]:::[\![e_2]\!]:::+):::[\![e_3]\!]:::+):::[\![e_4]\!]:::+ \end{equation*}$

Consider standard purely functional list implementation

EmptyList ::: ys = ys
(x::xs)   ::: ys = x::(xs ::: ys)

How many times is 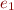$e_1$ traversed in such implementation?

quadratic behavior

Consider the related StringBuilder

Imperatively Producing Sequences

Mutable variable contains code so far

Instead of appending lists of instructions, append each instruction to code so far

Just like pretty printing using 'println' instead of our Printing Prefix Infix Postfix

Advantage: very efficient

Disadvantage:

less modular
translation order is instruction order
- must be careful
- yet works well and is natural

var code : Array[Instruction]
var last : Int = 0
 
def emit(i : Instruction) = {
  code(last) = i
  last = last + 1
}
 
def translate(e : Expr) = e match {
  case Mul(e1,e2) =>
    translate(e1)
    translate(e2)
    emit(Imul())
  case IntLiteral(c) =>
    emit(Bipush(c))
  ...
}

Functionally Producing Sequences

Use accumulating parameter

standard technique in functional programming

Instead of

$\begin{equation*} transl : Tree \to List[Instruction] \end{equation*}$

have

$\begin{equation*} transl0 : Tree \to List[Instruction] \to List[Instruction] \end{equation*}$

such that

$\begin{equation*} transl\ t = reverse\ (transl0\ t\ List()) \end{equation*}$

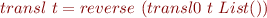
Rules for expressions:

$\begin{equation*} \begin{array}{l} transl0\ (e1 * e2)\ L = * :: (transl0\ e2\ (transl0\ e1\ L)) \\ transl0\ c\ L = \textbf{bipush}(c) :: L \end{array} \end{equation*}$

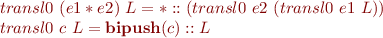
No concatenation anywhere, just adding to front.