Lecturecise 15: Type Checking Exercises

Problem 1

Consider the following grammar:

E ::= E+E
E ::= E*E
E ::= E=E
E ::= Num | true | false

where Num represents integers.

a) Consider the generalized CYK algorithm from

Lecturecise 11, slide 3

Run the algorithm on input:

1=2*3=true

checking whether it can be parsed. Show the content of the 'chart', that is, the set of triples 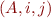$(A,i,j)$ , after the algorithm finishes.

b) How many parse trees can you extract from this chart?

c) Write down those parse trees that are correct according to the following types:

+ : Int x Int→Int

* : Int x Int→Int

= : Bool x Bool → Bool

= : Int x Int → Bool

d) Can you modify the CKY algorithm following the ideas from:

Lecturecise 12, slide 5-8

to introduce a semantic function $\mathbf{f}$ that computes only those trees that are correct according to the above types of operators?

e) What does the new algorithm return on the above input?

Problem 2

Determine if the following piece of codes type check according to the type rules.

Show all steps and give type derivation trees where applicable.

a) The class Array has a field length in which the length of the array is stored.

def swap(lst: Array[Int], a: Int, b: Int): Array[Int] = {
  if (a >= lst.length || b >= lst.length) lst else {
    val swap = lst(a)
    lst(a) = lst(b)
    lst(b) = swap
    lst
  }
}

Recall that we have the two type rules:

If $C$ is a declared subclass of $D$ , then $C <: D$
$\begin{equation*} \frac{\Gamma \vdash t: C \quad\quad C<:D}{\Gamma \vdash t: D} \end{equation*}$

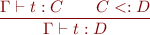
i) Give the type rule corresponding to new.
ii) Show this code typechecks.

class Shape
class Rectangle(width: Int, length: Int) extends Shape {
  def area : Int = width * length
}
class Square(length: Int) extends Rectangle(length,length)
new Square(5).area