Homework 03
Due Wednesday, 27 October, 10:10am. Please hand it in to Hossein before the beginning of the exercise session.
Problem 1
A context-free grammar is in Greibach two-standard form if productions are of the following form.
X -> aYZ X -> aY X -> a
- Prove that for any context-free grammar that does not contain ε there exists an equivalent Greibach two-standard grammar.
- Using the Greibach two-standard form prove that the class of context-free languages can be accepted by pushdown_automata.
Problem 2
Show that if a grammar is in Chomsky normal form then the parse tree for a word of length  has exactly
has exactly 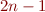 interior nodes.
interior nodes.
Problem 3
Assume a grammar in Chomsky normal has  non-terminals. Show that if the grammar can generate a word with a derivation having at least
non-terminals. Show that if the grammar can generate a word with a derivation having at least  steps, then the recognized language should be infinite.
steps, then the recognized language should be infinite.
Problem 4
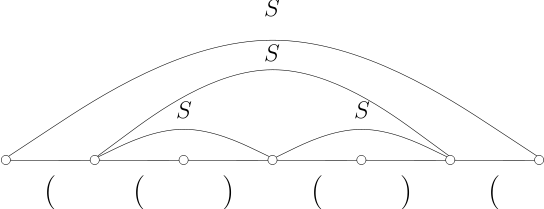
Assume that we want to use the CYK algorithm for the grammars which are not in Chomsky normal form. For example, consider the following grammar for balanced parenthesis.
S -> ( S ) S -> SS S -> ()
The diagram below shows the parsing for "(()())" using CYK.
Describe why it is not a good idea to use CYK for the arbitrary grammars not in the Chomsky normal form.
Problem 5
A production is called linear if it is of the form A → aBb. In other words, if the right hand side can contain only one non-terminal. Show that there are context free languages for which no linear grammar exists.