Homework 02

Due Wednesday, 20 October, 10:10am. Please Hand it in to Hossein before the beginning of the exercise session.

Problem 1

A grammar has a cycle if there is a non-terminal $A$ such that $A\stackrel{+}{\Rightarrow}A$ .

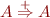Show that an LL(1) grammar must have no cycles.
Give an algorithm that eliminates cycles in a context-free grammar.

Problem 2

Show that the regular languages can be recognized with LL(1) parsers. Describe a process that, given a regular expression, constructs an LL(1) parser for it.

Problem 3

The following grammar is motivated by type definitions in Scala.

TypeDefinition  := "type" Identifier "=" Type
Type            := Type ","  Type
Type            := Type "=>" Type
Type            := "Int"  |  "Boolean"

By giving at least one input which has two different parse trees prove that the grammar is ambiguous.
Given the fact that “=>” has a lower precedence than “,” resolve the ambiguity of the grammar. That is, write a new grammar that determines the same language but is not ambiguous, such that the Type “Int ⇒ Int, Int” is parsed as function from Int to Int,Int.

Problem 4

The following grammar generates all the regular expressions over 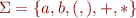$\Sigma = \{a,b,(,),+,*\}$ .

S -> S S
S -> S '+' S
S -> S '*'
S -> '(' S ')'
S -> 'a' | 'b'

Compute the First and Follow sets for S.
By giving two different parse trees for an input, show that the grammar is ambiguous.
Assuming that the '*' has the highest and '+' has the lowest precedence, rewrite the grammar to an unambiguous one.
Compute the First and Follow sets for the non-terminals of the new grammar.
Is the new grammar LL(1)?

Problem 5

A grammar is called LL(k) if it needs k tokens of lookahead when parsing a sentence. Does the following grammar belongs to LL(k) for any k?

S -> AB
S -> BC
A -> a
A -> Ba
B -> Cc
C -> c
B -> a