Exercises 10
In the following problems assume that we have a machine with the registers  .
.
All the registers and the integer numbers consist of 2 bytes.
We use the temporary variables x1 … x31 to implement our intermediate code. The goal is to assign each temporary variable xi to a register and to minimize the exploited registers.
Problem 1
The GCD of two numbers can be computed using the Euclid algorithm.
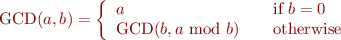
We can implement the GCD algorithm with temporary variables as the following.
x1 := a x2 := b Start: if x2 = 0 jump Done x3 := x1 % x2 x1 := x2 x2 := x3 jump Start Done: return x1
- Construct the control-flow graph
- Determine the set of live variables before and after the execution of each instruction.
- Construct the interference graph.
- Can coalescing help us to remove any move instructions?
Problem 2
Given a set of  numbers the variance is defined by the following formula.
numbers the variance is defined by the following formula.
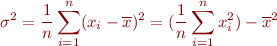
where  is the average of the numbers.
is the average of the numbers.
The following Scala function computes the variance of n numbers which is passed through the array a.
def variance(a: Array[Int], n: Int): Int = { var sum = 0 var squares = 0 for (i <- 0 until n) { sum += a(i) squares += a(i) * a(i) } val average: Int = sum / n val result: Int = (squares / n) - (average * average) return result }
We can sketch the translation of the variance function to instruction level with temporary variables as the following.
| Instruction | Explanation |
|---|---|
| x1 := &a | // pointing to the beginning of the array: a(0) |
| x2 := 0 | // sum |
| x3 := 0 | // squares |
| x4 := 0 | // loop counter: i |
| x5 := n | // the length of the array: n |
| L: x6 := *x1 | // beginning of the loop |
| x2 := x2 + x6 | // accumulate sum |
| x7 := x6 * x6 | |
| x3 := x3 + x7 | // accumulate average |
| x1 := x1 + 2 | // pointer to the next element |
| x4 := x4 + 1 | |
| if(x4 < x5) jump L | // closing of the loop |
| x8 := x2 / x5 | // average |
| x9 := x3 / x5 | // average of squares |
| x10 := x8 * x8 | // square of averages |
| x11 := x9 - x10 | // result |
| return x11 |
- Construct the control-flow graph
- Determine the set of live variables before and after the execution of each instruction.
- Construct the corresponding interference graph.
- How many colors is needed to color the graph without spilling?
- Give a minimal register allocation.