Exercises 02
Exercise 1
The dangling-else problem happens when the conditional statements are parsed using the following grammar.
S := "if" E "then" S S := "if" E "then" S "else" S
Find an unambiguous grammar that accepts the same conditional statements and matches the else statement with the nearest unmatched if.
Exercise 2
We call a production rule “left recursive” if it is of the form  . Similarly a right recursive rule is defined as
. Similarly a right recursive rule is defined as  .
Show that any context free grammar that contains both left and right recursive rules for a single LHS nonterminal should be ambiguous.
.
Show that any context free grammar that contains both left and right recursive rules for a single LHS nonterminal should be ambiguous.
Exercise 3
Compute the First and Follow sets for the nonterminals of the following grammar 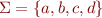 .
.
S -> SAa | ε A -> ABb | ε B -> BCc | ε C -> d
Exercise 4
The following grammar recognizes the language 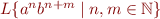 .
.
S -> aSb | A A -> bA | ε
Show that no predictive descent parser can correctly predict the correct production rule for every element of  .
.