LARA

Exercises 01

Exercise 1

Convert the following NFAs to deterministic finite automata.

a) b)

Exercise 2

Design a DFA which accepts all the binary numbers divisible by 6. For example your automaton should accept the words 0, 110 (6 decimal) and 10010 (18 decimal).

Exercise 3

Assume the following extensions to the regular expressions. In each case describe why the modification does not actually change the expressibility.

  • The intersection of two regular expressions.
  • The optional expression 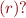$(r)?$ denoting that expression $r$ optional
  • Limiting Kleene repetition with a maximum and minimum bound

Design your own operator for regular expressions to make it expressible for describing nested comments.

Exercise 4

Integer literals are in three forms in Scala: decimal, hexadecimal and octal. The compiler discriminates different classes from their beginning. Decimal integers are started with a non-zero digit. Hexadecimal numbers begin with 0x or 0X and may contain the digits from 0 through 9 as well as upper or lowercase digits A to F afterwards. If the integer number starts with zero, it is in octal representation so it can contain only digits 0 through 7. There can be an l or L at the end of the literal to show the number is Long.

  • Draw a single DFA that accepts all the allowable integer literals.
  • Write the corresponding regular expression.

Exercise 5

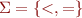Let $L$ be the language of strings on $\Sigma = \{<,=\}$ defined by 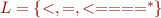$L = \{<,=,<====^{*}\}$ that is, $\{ <, = \} \cup \{ <=^{n} \mid n \ge 3 \}$.

  • Construct a DFA that accepts $L$.
  • Describe how the lexical analyzer will tokenize the following inputs.
    • <=====
    • ==<==<==<==<==
    • <=====<

Exercise 6

For each of the following languages find the first set. Determine if the language is nullable.

(a+b)*(b+d)((c+a+d)* + a*)

Exercise 7

Homomorphism is function from letters to strings such that 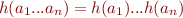$h(a_1 ... a_n) = h(a_1) ... h(a_n)$

  • Prove if language $L$ is regular then $\{ h(w) \mid w \in L \}$ is regular.
  • Using Pumping Lemma prove that the language $\{a^n.b^n \mid n\in\mathbb{N}\}$ is not regular.
  • Prove that equally many digits before and after decimal point is not regular.