static int x;
static int y;
static int z;
static int res;
 
int f() {
  res = x * y + y * z + x * z;
}

We compile it for X86 instruction set, using

gcc -S xyz.c

Essential part:

movl    x, %edx
movl    z, %eax
addl    %eax, %edx
movl    y, %eax
movl    %edx, %ecx
imull   %eax, %ecx
movl    x, %edx
movl    z, %eax
imull   %edx, %eax
leal    (%ecx,%eax), %eax   /* load effective address, used as add */
movl    %eax, res

Full assembly listing:

        .file   "xyz.c"
        .text
.globl f
        .type   f, @function
f:
        pushl   %ebp
        movl    %esp, %ebp
        movl    x, %edx
        movl    z, %eax
        addl    %eax, %edx
        movl    y, %eax
        movl    %edx, %ecx
        imull   %eax, %ecx
        movl    x, %edx
        movl    z, %eax
        imull   %edx, %eax
        leal    (%ecx,%eax), %eax
        movl    %eax, res
        popl    %ebp
        ret
        .size   f, .-f
        .local  x
        .comm   x,4,4
        .local  y
        .comm   y,4,4
        .local  z
        .comm   z,4,4
        .local  res
        .comm   res,4,4
        .ident  "GCC: (GNU) 4.1.3 20070929 (prerelease) (Ubuntu 4.1.2-16ubuntu2)"
        .section        .note.GNU-stack,"",@progbits

With -O3 option - note each variable loaded once, and there are only two multiplications:

	movl	x, %ecx
	movl	z, %edx
	pushl	%ebp
	movl	%esp, %ebp
	popl	%ebp
	leal	(%edx,%ecx), %eax
	imull	%ecx, %edx
	imull	y, %eax
	addl	%edx, %eax
	movl	%eax, res
	ret

We applied distributivity law:

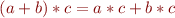
Does the above distributivity law hold for 32-bit machine integers?

• prove or give a counterexample
• what is the definition of machine arithmetic operations using mathematical notation the distributivity holds, thanks to laws of modular arithmetic
• what does this evaluate to:

var x = Int.MaxValue
x < x + 1

Does the above distributivity law hold for floating point numbers?

• prove or give a counterexample

var a : Double = 1.0 + 1.0e-15
var b : Double = -1.0
var c : Double = 1.23456789
println((a + b)*c)
println(a * c + b * c)

1.3706456969408975E-15
1.3322676295501878E-15

See the floating point standard.