Using Finite State Machines to Build Lexers

Suppose we have token classes 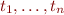$t_1,\ldots,t_n$ and each $t_i$ is given by regular expression $r_i$ .

Consider building an automaton for 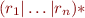$(r_1 | \ldots | r_n)*$

a step towards solution

Example: Construct (directly) a finite state machine for these classes of tokens:

<, >, =, <=, =>, >=, ==, <=>

Verify whether it is minimal. Run it on the sequence

<==><==<=>

What can this automaton tell us about input character stream? it can say whether it represents a sequence of valid tokens or not.

What we need is to compute the sequence of tokens

Modify state machine

for each accepting state specify the token recognized (but do not stop)
- use token class priority if multiple options
for longest match rule: remember last token and input position for last accepted state
when no accepting state can be reached (effectively: when we are in a trap state)
- revert position to last accepted state
- return last accepted token

Example: How to modify previous example to store the information needed?

Remark: Do not stop the running machine as soon as you are not in an accepting state, even if you have already gone through an accepting state. Wait until the machine gets entirely stuck, to be sure that it is not possible to find a longer token in the future.