Type Rules using Environment
To know types of variables, type rules must refer to the environment.
Notation

means that in environment  , expression
, expression  is type correct and has type
is type correct and has type 
 is a partial function from names (of variables, operators, and methods) to types
is a partial function from names (of variables, operators, and methods) to types
Shorthand 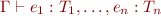 means
means  for
for 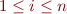
Variable rule with environment:
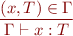
Function application rule with environment:
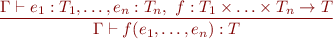
Example:
{(x,int)} |- x : int, {(x,int)} |- 7 : int
----------------------------------------------
{(x,int)} |- (x+7) : int
Type Rule for Entire Program
Given a program
class World {
Tg_1 xg_1;
...
Tg_n xg_n;
method1
...
methodM
}
The program is type correct if each method is type correct:
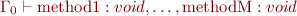
where the initial environment 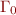 contains:
contains:
- types of predefined operators like
 ,
,  ,
,  and constants
and constants  ,
,  ,
,  ,
, 
- types of global variables,
 for each global variable declaration
for each global variable declaration 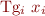
- types of declared methods: for each method definition
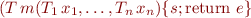
the environment  contains binding
contains binding
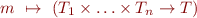
Example:
class World {
int x;
int y;
def inc() {
x = x + y;
return;
}
}
Initial environment G0 contains {(x,int),(y,int),(+,int x int → int)}. While type checking body in this environment, we will have
G0 |- x : int, G0 |- y : int,
G0 |- + : int x int -> int
-------------------------------
G0 |- x + y : int
Type Rule for Method Bodies
Note that environment  already contains the expected type that the method is supposed to have.
already contains the expected type that the method is supposed to have.
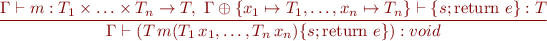
Here
 denotes overriding one map with another, as seen in Notation for Maps
denotes overriding one map with another, as seen in Notation for Maps- we give a dummy 'void' type to indicate that method is well-defined
- the assumption of type rule checks that the return type is correct
- later we present more elegant approach using lambda calculus