LARA

Translation Correctness for Expressions

Recall Evaluating Postfix

Notation

Functions:

  • evaluation: $eval\ :\ Expression \to Int$
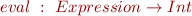
  • compilation: $[\![ \_ ]\!]\ :\ Expression \to List[Instruction]$
  • virtual machine: $run\ : \ List[Instruction] \to List[Int] \to List[Int]$

For simplicity we will omit environments mapping variables

  • does not affect this proof

We often write X instead of List(X) when X is one element

Also, we often use same symbol '*' for

  • operator in the tree
  • operator in instruction sequence
  • corresponding mathematical operator

Key Facts

Evaluation of expressions:

\begin{equation*} eval(e_1 * e_2) = eval(e_1) * eval(e_2) \end{equation*}

Translation:

\begin{equation*} [\![ e_1 * e_2 ]\!] = [\![e_1]\!] ::: [\![e_2]\!] :::\ {*} \end{equation*}

Here

  • the last occurrence of is the imul instruction
  • $e_1*e_2$ denotes a tree with node type $*$ and children $e_1$, $e_2$

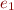run-virtual machine: From definition of $run$ and by induction on 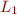$L_1$,

\begin{equation*} run\ (L_1 ::: L_2)\ S = run\ L_2\ (run\ L_1\ S) \end{equation*}

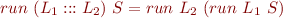
Of course

\begin{equation*} run\ (* ::: L)\ (S:::x_1:::x_2) = run\ L\ (S:::x) \end{equation*}

where $x$ is the result of computing $x_1*x_2$, and

\begin{equation*} run\ (c ::: L)\ S = run\ L\ (S:::c) \end{equation*}

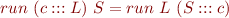
for constant $c$, and

\begin{equation*} run\ EmptyList\ S = S \end{equation*}

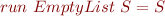
Correctness Theorem

For every $e$,

\begin{equation*} run\ [\![ e ]\!]\ List()\ \ =\ \ List(eval(e)) \end{equation*}

Attempt at Inductive Proof

Induction on structure of $e$

\begin{equation*}\begin{array}{l} run\ [\![e_1 * e_2]\!]\ S = \\ run\ ([\![e_1]\!] ::: [\![e_2]\!] ::: *)\ S = \\ run\ ([\![e_2]\!] ::: *)\ (run\ [\![e_1]\!]\ S) = \\ ? \end{array}\end{equation*}

Induction Hypothesis

For every expression $e$ and every list of integers $S$,

\begin{equation*} run\ [\![ e ]\!]\ S\ \ =\ \ S ::: eval(e) \end{equation*}

Inductive Proof

\begin{equation*}\begin{array}{l} run\ [\![e_1 * e_2]\!]\ S = \\ run\ ([\![e_1]\!] ::: [\![e_2]\!] ::: *)\ S = \\ run\ ([\![e_2]\!] ::: *)\ (run\ [\![e_1]\!]\ S) = \\ run\ ([\![e_2]\!] ::: *)\ (S ::: eval(e_1)) = \\ run\ (*)\ (run\ [\![e_2]\!]\ (S ::: eval(e_1))) = \\ run\ (*)\ (S ::: eval(e_1) ::: eval(e_2)) = \\ S ::: (eval(e_1) * eval(e_2)) = \\ S ::: eval(e_1 * e_2) \end{array}\end{equation*}