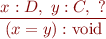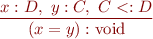Subtyping for Assignments and Soundness Idea
Consider a language with
- classes containing methods
- subclassing
- assignments of local variables
Example:
class C { def m = {...} } class D extends C { def n = {...} } // thus, D <: C class Main { def main = { var x : D = new D var y : C = new C // y = x ? // x = y ? x.n y.m } }
Goal: ensure when x.m is invoked, then x is an object whose class has a method m defined.
- in machine code a call to non-exissting method could correspond to jumping to a potentially arbitrary location in memory!
- if we do a run-time check then our program could crash with a form of “unknown method” exception
How can we design the type system that is sound for ensuring this property?
Example: consider call y.m
During type checking, y will be assigned its declared type (here: C).
Let us require that the declared type contains m.
We therefore need the following property:
- if an object has some declared type C, then during execution it can only point to objects that contain all those methods that are contained in C
To ensure the previous property we require the following subtyping invariant to hold during program execution:
- if an object has declared type C, then it can store only objects that extend C (in one or more steps)
This invariant will ensure that we do not call non-existing methods
Consider
D extends C var x : D var y : C
Which assignments preserve the invariant:
What is the rule for assignment