LR Parsing with Lookahead Items

Although SLR Parser Actions use lookahead, their finite state machine is computed without considering lookahead

LR(k) parser uses more general LR(k) items

We explain LR(1)

LR(1) item is (X::=p.q,a), written

X ::= p.q    a

where

X::=p.q is a dotted production (LR(0) item)
p symbols are already represented on the stack
'a' is token, such that remaining tokens in input are of the form 'qa'

Starting State

The start state is the closure of the item (S' → .S EOF, a).

Here the symbol a can be chosen arbitrarily, because the parser will never reduce the first rule, the parsing can finish when it reaches (S' → S. EOF, a) and the current input is EOF.

Closure and Goto for Sets of LR(1) Items

They generalize such functions for LR(0) parser in Automata for LR Parsing without Lookahead

closure(I) uses first(…) function to select correct lookahead

closure(I) is least set such that

I $\subseteq$ closure(I)
if (Y::=r) is a rule, 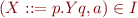$(X::=p.Yq, a)\in I$ , and w $\in$ first(qa), then (Y::=.r, w) $\in$ closure(I)

goto is entirely analogous as before (using new closure):

$\begin{equation*} goto(I,X) = closure(\{ (Y::=qX.r,a) \mid (Y::=q.Xr,a)\in I \}) \end{equation*}$

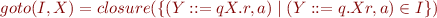
LALR(1) Items

The set of reachable LR(1) states can be large

LALR(1) uses a smaller set of states by merging some LR(1) states

Let nolook(I) denote removal of lookahead

$\begin{equation*} nolook(I) = \{(X::=p.q) \mid (X::=p.q, a) \in I \} \end{equation*}$

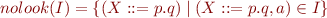
then if nolook(I)=nolook(J), we merge I and J (and replace them with $I \cup J$ )

Note: this is better than SLR because

we first compute automaton using lookahead items
only then merge them

This is a popular approach

well-known 'yacc' parser generator