LARA

LL(1) Table-Driven Parsing Overview

First, compute nullable, first, follow

Then, make parsing table which stores the alternative, given

  • non-terminal being parsed (in which procedure we are)
  • current token

Given (X ::= 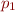$p_1$ | … | $p_n$) we insert alternative j into table iff

  • t $\in$ first(p_j), or
  • nullable($p_j$) and t $\in$ follow(X)

If in parsing table we have two or more alternatives for same token and non-terminal:

  • we have conflict
  • we cannot parse grammar using recursive descent

Otherwise, we say that the grammar is LL(1)

  • Left-to-right parse (the way input is examined)
  • Leftmost derivation (expand leftmost non-terminal first–recursion in descent does this)
  • (1) token lookahead (current token)

What about empty entries?

  • they indicate errors
  • report that we expect one of tokens in
    • first(X), if X $\notin$ nullable
    • first(X) $\cup$ follow(X), if X $\in$ nullable