LARA

Full Employment Theorem for Compiler Writers

Informal Statement

The problem of given a program $p$ and a property $N$ that is true for some programs and false for other programs, check (precisely) whether program satisfies $N$ is undecidable if property $N$ talks only about the values computed by the program and program termination (and not e.g. how the values are computed).

This follows from Rice's theorem which follows from the undecidability of the Halting problem

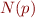  • to check if $c$ terminates, we build a program $p$ such that $N(p)$ and a program $cp$, that behaves like $p$ if $c$ does not terminate, and otherwise $\lnot N(cp)$

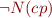
Consequences

Examples of undecidable problems:

  • can a given program reach a state where null dereference happens
  • is a given variable dynamically alive at a given program point in a given program
  • is the given variable initialized before the execution reaches a given program point
  • are the values of two given variables equal in all executions of the program
  • does the given assertion evaluate to 'true' in all executions of a given program
  • …

How can we then build compilers?

  • we do not attempt to answer this question precisely
  • we either compute an answer, or we say “we do not know”
  • we say compilers do “conservative” static analysis

In initialization analysis, output is:

  • variable is definitely initialized
  • variable is possibly un-initialized (either it is un-initialized, or it is initialized but it is too hard to see why)

In live-variable analysis, output is:

  • variable is definitely not live
  • variable is live (it is either dynamically live, or it is not dynamically live but it is difficult to see why)

Proof Sketches

Halting Problem Undecidability Theorem (Turing): There is no program $H$ (think of it as analyzer that checks if programs are terminating) that takes as input a representation of an arbitrary program $P$ and the input of the program $X$, and determines whether $P$ will terminate its computation if we ran $P$ on input $X$.

Proof sketch: This is a proof by a diagonal argument. Suppose that we do have such program $H$. Then define the following program that takes program descriptions $Y$ as input: 

def F(Y) = if H(Y,Y) then (while(true){}) else true

The question is then whether running 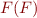$F(F)$ will terminate. There are two cases, either 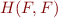$H(F,F)$ holds, or not.

If 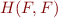$H(F,F)$ holds, then 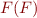$F(F)$, by definition of $F$ enters the 'true' branch and thus executes 

  while(true){}

Thus, 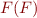$F(F)$ does not terminate. But this is in contradiction with the definition of 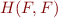$H(F,F)$, which says that $F$ terminates on input $F$.

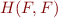If $H(F,F)$ does not hold, it then 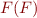$F(F)$ goes to 'else' branch and terminates. But this is in contradiction with the definition of 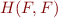$H(F,F)$ being false, which says that $F$ should not terminate on input $F$.

Impossibility of detecting dead code: There is no program 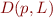$D(p,L)$ (think of it as data-flow analyzer) that can take as an input a program $p$ and a program location $L$, whether there exists an execution of $X$ that reaches $L$.

Proof sketch: By reduction to previous theorem. We can always transform a given program $p$ into a program that always terminates in its last location (all 'halt' and 'exit' instructions are replaced by a jump to end of the program). Suppose p0 is such a program. To check if p0 terminates on an input $X$, we consider the program 

def p = {
   p0
L: {}
}

Clearly, if p0 terminates, then it will execute L. Conversely, if p0 does not terminate, it will never reach L. Therefore, checking if 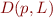$D(p,L)$ would tell us whether p0 terminates. By Halting problem, this is undecidable, so $D$ cannot exist. QED

Impossibility of checking assertions: There is no program 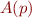$A(p)$ that will accept a program $p$ containing assertions and check whether these assertions are true in all executions.

Proof: By reduction to previous theorem. Given a program $p$ with assertions, we introduce a fresh location L and replace each assertion 

  assert(c)

with the condition 

if (!c) {
  goto L
}

Then the assertions are true in all executions if and only if program never reaches location $L$. QED