Designing Correct Data-Flow Analyses
We describe guidelines to design a correct analysis for a set of properties of interest
Define Properties of Interest
Define precisely what property is needed (depends on the application), e.g.
- absence of errors
- improving code performance without changing program meaning
Recall Applications of Data-Flow Analysis
Example: every variable assigned before being read
Define Analysis (Semi)Lattice to Express Properties
Find a lattice that
- encodes properties of interest
- enables terminating analysis
Specify lattice top, bottom, join
Precisely Specify Meaning of Lattice Elements
Specify concretization function, mapping lattice elements to sets of states
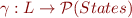
In SignAnalysis.scala, we have for 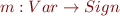 for
for 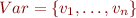
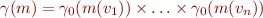
where, assuming infinite integers we have
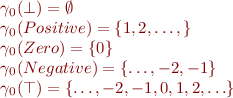
Monotonicity requirement for  :
:
 implies
implies  , for all
, for all 
Note that this implies
Example
Lattice element  given by
given by 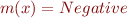 ,
, 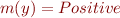
Then
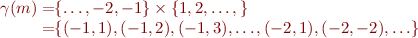
Here we wrote 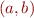 to mean the function
to mean the function 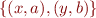 .
.
Compute a Sound Initial Lattice Element
Initially, the set of reachable states is empty at all points, except at CFG entry, where we have set of initial states of program 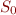
In the initial state of data-flow analysis, we will assign  to each program location except entry
to each program location except entry
At program entry we assign a lattice element  such that
such that
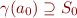
Putting  to
to  is always safe (this corresponds to assuming any possible program states at program initialization time). If we know something more about the initial program states, we can give better initial element. For sign analysis, if we assume all variables are initialized to 0, then we can set
is always safe (this corresponds to assuming any possible program states at program initialization time). If we know something more about the initial program states, we can give better initial element. For sign analysis, if we assume all variables are initialized to 0, then we can set 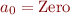 .
.
Derive Sound Transfer Functions
For each statement 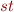 , define
, define 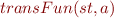
Needs to correctly approximate the effect of statement 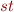 on states given by
on states given by  .
.
Formally, for all statements 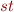 and lattice elements
and lattice elements  the Correctness Condition is:
the Correctness Condition is:
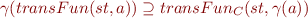
Here 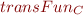 is the transfer function from Concrete Execution as Data-Flow Analysis
is the transfer function from Concrete Execution as Data-Flow Analysis
- takes set of states and runs statement
 on each state
on each state
Recall SignAnalysis.scala transfer functions
Running the Algorithm
As described in DataFlowAnalysis.scala, we execute this iteration
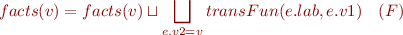
The algorithm terminates because the elements get larger and larger.
When the algorithm terminates we know that the above assignment is in fact a true as an equation (not assignment).
Sketch of Correctness Proof
Here is why the computed result, given by 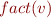 for each vertex
for each vertex  is correct.
is correct.
Consider any execution of the program represented as control-flow graph (CFG). The execution goes through states, which we can describe by the vertex  and the values of variables
and the values of variables 
The execution is a path in CFG, starting at 'entry' and finishing at 'exit'. Consider the resulting alternating sequence of vertices and CFG statements:
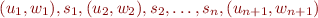
where 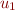 = 'entry',
= 'entry', 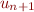 ='exit'.
='exit'.
We prove by induction on  claim that, for each
claim that, for each  ,
,
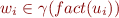
In other words, the values  of variables at each program point
of variables at each program point  are correctly described by the lattice value
are correctly described by the lattice value 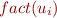 at that program point.
at that program point.
Proof:
Base case: this is how we chose  .
.
Inductive step: follows from
- Monotonicity of

- Correctness Condition of

- The condition that
 map has stabilized
map has stabilized
Indeed:
- suppose
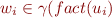 by inductive hypothesis
by inductive hypothesis - then by definition,
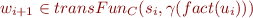 because it is a next step in program execution
because it is a next step in program execution - by Correctness Condition,
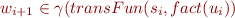
- because
 stabilized,
stabilized, 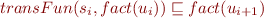 ; indeed,
; indeed, 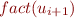 is an upper bound of values on right-hand side of equation
is an upper bound of values on right-hand side of equation 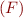
- by Monotonicity of
 , we obtain
, we obtain 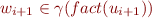 . QED
. QED
Note: for correctness, it does not matter how we obtained fact, as long as we have checked that it stabilized (we could have guessed those values or found not-necessarily least solution).