LARA

Computing Follow Sets

The Need for Follow

What if we have 

X = Y Z | U

and U is nullable? When can we choose a nullable alternative (U)?

  • if current token is either in first(U) or it could follow non-terminal X

t is in follow(X), if there exists a derivation containing substring X t

Example of language with 'named blocks': 

statements ::= "" | statement statements
statement ::= assign | block
assign ::= ID "=" (ID|INT) ";"
block ::= "beginof" ID statements ID "ends"

Try to parse 

beginof myPrettyCode
  x = 3;
  y = x;
myPrettyCode ends

Problem parsing 'statements':

  • identifier could start alternative 'statement statements'
  • identifier could follow 'statements', so we may wish to parse “”

Computing follow(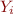$Y_i$), given rule X = $Y_1$ … $Y_i$ … $Y_j$ … $Y_k$

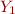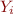  • add first($Y_j$), if $Y_{i+1}$,…,$Y_{j-1}$ are all nullable
  • add follow($X$), if $Y_{i+1}$, …, $Y_k$ are all nullable

Possible computation order:

  • nullable
  • first
  • follow

Example: compute these values for grammar above 

follow = {}
first
  statements {ID, "beginof"}
  statement  {ID, "beginof"}
  assign     {ID}
  block      {"beginof"}
follow
  statements {ID}
  statement  {ID, "beginof"}
  assign     {ID, "beginof"}
  block      {ID, "beginof"}

The grammar cannot be parsed because we have 

statements ::= "" | statement statements

where

  • statements $\in$ nullable
  • first(statements) $\cap$ follow(statements) = {ID} $\neq \emptyset$

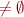
If the parser sees ID, it does not know if it should

  • finish parsing 'statements' or
  • parse another 'statement'