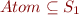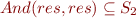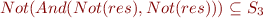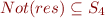LARA

This is an old revision of the document!

Set Constraints for Algebraic Datatype Inference

We want that our compiler detects correctly the possible subset of types for each function.

Example

Using the following grammar : 

type form = Atom of string
          | And of form*form
          | Or of form*form
          | Not of form

we can have the following types : 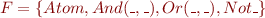$F = \lbrace Atom, And(\_ , \_), Or(\_ , \_), Not \_ \rbrace$ which is an infinite set (“_” represents any kind of type).

But if we define the following function : 

let rec elimOr(f : form) : form =
    match f with
 S1: | Atom s -> Atom s
 S2: | And(f1,f2) -> And(elimOr f1, elimOr f2)
 S3: | Or(f1,f2) -> Not(And(Not(elimOr f1), Not(elimOr f2)))
 S4: | Not(f1) -> Not(elimOr f1)

It is clear that the output types of this function is a subset of $F$ (as the $Or$ is removed). In fact, if we define $res$ as the resulting type of this function, $res$ can be computed by computing the fixpoint of : $S_1 \cup S_2 \cup S_3 \cup S_4 \subseteq res$

  1. $Atom \subseteq S_1$
  2. $And(res, res) \subseteq S_2$
  3. $Not(And(Not(res), Not(res))) \subseteq S_3$
  4. $Not(res) \subseteq S_4$

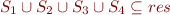
In this particular case, the fixpoint is : 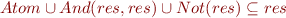$Atom \cup And(res, res) \cup Not(res) \subseteq res$ which computes correctly the fact that the $Or$ has been removed.