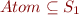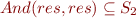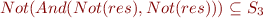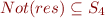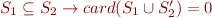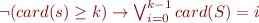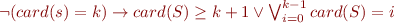Lecture 23: Analysis of procedures, objects, and pointers

Announcements:

semester and master's projects
SAV07 mini projects

Analysis of object-oriented languages

* Fast and Effective Optimization of Statically Typed Object-Oriented Languages (includes description of Rapid Type Analysis algorithm)

Example of the problem

Given the following object-oriented code :

class A {
  m(){...}
}
class B extends A {
  m(){...}
}

and given the following execution :

A x;
x = new A();
x = new B();
x.m();

then we cannot know statically which function m will be called here.

Solving this problem is difficult. As we do not want to spend too much time on checking, the solution will be quite simple (but less than previous work).

Possible Methods (from simplest to more complex) :

Trivial Analysis (TA) : We suppose that each method as a unique name
Ckass Hierarchy Analysis (Cha) : We build the hierarchy and search in all these classes
Rapid Type Analysis (RTA) : We look only at instanciated classes

RTA

In order to do this, one has first to determine the classes that can be called. This means that one has to build the Call Graph and bound it to the part we want to analyse. Producing the best graph can be arbitrarly complicated !

Problems :

Using this graph we can analyze only this subset of the whole graph.
It do not even take the order of the commands into account

RTA using Set Constraints

Defining

M : the set of procedure bodies
P : the set of call sites
T : the types

We use the following functions :

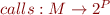$calls : M \rightarrow 2^P$ : all the program points of $m \in M$ where a call occurs
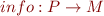$info : P \rightarrow M$ : the method that is called according to declared type
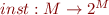$inst : M \rightarrow 2^M$ : instanciated methods (contained in the instanciated type) in m
$over : M \rightarrow M \cup \lbrace \bot \rbrace$ : the method that overrides m

We can then introduce 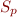$S_p$ as the set variable of the called methods :

$\begin{equation*}\forall p \in P . S_p \subseteq \left \lbrace m | \left ( info(p), m \right ) \in r^*, r = \lbrace (x,y) | x = over(y) \rbrace \right \rbrace \end{equation*}$

We also define 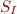$S_I$ as the set of all possibly called methods that we can build using the following formula :

$\begin{equation*} main \in S_I \bigwedge_{m \in M} \left ( m \in S_I \wedge p \in calls(m) \right ) \Rightarrow S_p \subseteq S_I \bigwedge_{m \in M} m \in S_I \Rightarrow inst(m) \subseteq S_I \end{equation*}$

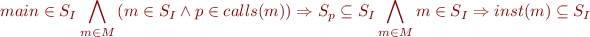
Type Checking using Set Constraints

We want that our compiler detects correctly the possible subset of types for each function.

Example

Using the following grammar :

type form = Atom of string
          | And of form*form
          | Or of form*form
          | Not of form

we can have the following types : 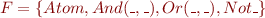$F = \lbrace Atom, And(\_ , \_), Or(\_ , \_), Not \_ \rbrace$ which is an infinite set (“_” represents any kind of type).

But if we define the following function :

let rec elimOr(f : form) : form =
    match f with
 S1: | Atom s -> Atom s
 S2: | And(f1,f2) -> And(elimOr f1, elimOr f2)
 S3: | Or(f1,f2) -> Not(And(Not(elimOr f1), Not(elimOr f2)))
 S4: | Not(f1) -> Not(elimOr f1)

It is clear that the output types of this function is a subset of $F$ (as the $Or$ is removed). In fact, if we define $res$ as the resulting type of this function, $res$ can be computed by computing the fixpoint of : $S_1 \cup S_2 \cup S_3 \cup S_4 \subseteq res$

$Atom \subseteq S_1$
$And(res, res) \subseteq S_2$
$Not(And(Not(res), Not(res))) \subseteq S_3$
$Not(res) \subseteq S_4$

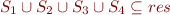
In this particular case, the fixpoint is : 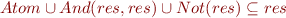$Atom \cup And(res, res) \cup Not(res) \subseteq res$ which computes correctly the fact that the $Or$ has been removed.

This example shows that we can use set constraints to create type systems ! Read the following papers for more information :

Type inference. Semantics of untyped lambda calculus.
Soft typing with conditional types

Modularity: Componential set-based analysis

Deciding set constraints

Some approaches:

simplification algorithms - most efficient for tractable classes
techniques specific to set constraints (using hypergraphs, The complexity of set constraints)
reduction to monadic class of first-order logic (Set constraints are the monadic class)
regular tree grammars and tree automata (Practical aspects of set based analysis)
reduction to term algebras (First-order theory of structural subtyping)

Term Algebras

$L = \lbrace a, f, \ldots \rbrace$
$H$ : set of all ground terms
First-order theory : $\forall x \exist y . f(f(a,a), x) = f(y, a) \wedge y \neq a$

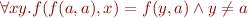
This is First-Order Logic (FOL) with variables ! We can relate this to set constraints

Monadic Class of FOL

MFOL¹⁾ has : only unary predicates, no function symbol, quatifiers and logic.

Translating this to our sets language :

F := S = S
   | S ⊆ S
   | card(S) ≥ k
   | card(S) = k
   | F ∧ F
   | ¬ F
   | ∃v.F
S := v
   | S ∪ S
   | S ∩ S
   | S'
   | ∅
   | 1

Where :

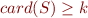$card(S) \geq k$ is syntactic sugar to represent a unary operator, as $k$ is not a variable, that compare the cardinality of $S$ with $k$
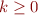$k \geq 0$ is an integer
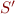$S'$ is the complement set of $S$
$1$ represents the whole universe

In order to agree with our definitions of set constraints, we need to eliminate :

$S_1 = S_2 \rightarrow S_1 \subseteq S_2 \wedge S_2 \subseteq S_1$
$S_1 \subseteq S_2 \rightarrow card(S_1 \cup S_2') = 0$

We then have to be able to represent the following formulas :

$\neg(card(s) \geq k) \rightarrow \bigvee_{i=0}^{k-1} card(S) = i$
$\neg(card(s) = k) \rightarrow card(S) \geq k+1 \vee \bigvee_{i=0}^{k-1} card(S) = i$

We can then perform quantifier elimination. Note that this is not possible in case we do not have the $card$ operator : \begin{equation*}\exists v.card(S_1 \cap v) = k_1 \wedge card(S_1 \cap v') = k_2 \Rightarrow card(S_1) = k_1 + k_2\]

After elimination of the quantifiers, deciding the result of the formula is trivial.

¹⁾

Set constraints are the monadic class