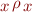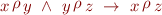Preorder
A (reflexive) preorder relation  on set
on set  is a binary relation
is a binary relation 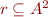 that is reflexive and transitive, that is, these two properties hold:
that is reflexive and transitive, that is, these two properties hold:
Constructing a partial order from a preorder
Intuitively, preorder differs from partial order in that there are distinct elements that have same ordering properties with respect to other elements. For such elements we therefore have  and
and  . By identifying these elements we obtain a partial order.
. By identifying these elements we obtain a partial order.
More precisely, let  be a preorder. Define relation
be a preorder. Define relation  by
by
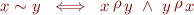
It is easy to verify that  is an equivalence relation. Moreover, if we define relation
is an equivalence relation. Moreover, if we define relation  on equivalence classes by
on equivalence classes by
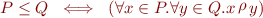
for  , then we can prove that
, then we can prove that  is a partial order.
is a partial order.