LARA

Lambda calculus

This is a very brief introduction to lambda calculus.

Lambda calculus is a notation for defining functions. It is very simple and powerful. Two of its main uses are

  • foundation of programming languages, especially functional languages such as Ocaml, Haskell, and Scala
  • higher order logic notations, such as Isabelle, HOL, PVS

For example, a function which takes its argument and increments it by 2 is given by lambda expression $\lambda x.x+2$. The $\lambda$ operator is a binder used to indicate that a variable is to be treated as an argument of a function. We indicate function application by juxtaposition. Here are some example expressions and their values:

\begin{eqnarray*} (\lambda x. x + 2)\, 7 &=& 9 \\ ((\lambda x. (\lambda y. x - y))\, 5)\, 3 &=& (\lambda y. 5 - y) 3 = 5 - 3 = 2 \\ (((\lambda f. (\lambda x. f(f x))) (\lambda y. y^2))) 3 &=& (\lambda x. (\lambda y. y^2) ((\lambda y.y^2) x))) 3 = (\lambda y. y^2) ((\lambda y.y^2) 3) = (\lambda y.y^2) 9 = 81 \end{eqnarray*}

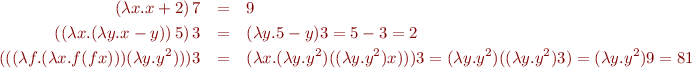
Note: in Isabelle and Jahob notation we use '% x.F' or '\<lambda> x.F' to denote $\lambda$.F binder. In ocaml, one can use 'function x → F', and in Haskell one can use '\ x → F'.

Lambda expressions

Untyped lambda expressions are given by following grammar:

\begin{equation*}\begin{array}{l} T ::= v \mid \lambda v.T \mid T\, T \\ v ::= v_1 \mid v_2 \mid ... \end{array}\end{equation*}

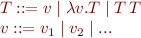
That is, an expression is a variable, a lambda expression defining a function, or an application of one expression to another.

Beta reduction

The main rule of lambda calculus is beta reduction, which formalizes function application:

\begin{equation*} (\lambda x. s) t = s[x:=t] \end{equation*}

where we assume capture-avoiding substitution.

One simple use of lambda expressions to introduce shorthands: instead of writing

\begin{equation*} \mbox{let}\ x = E\ \mbox{in}\ F \end{equation*}

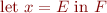
we can write

\begin{equation*} (\lambda x.F)E \end{equation*}

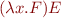
References: