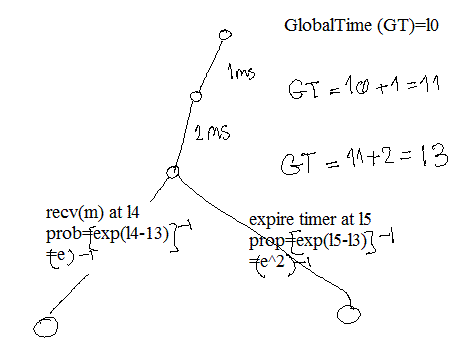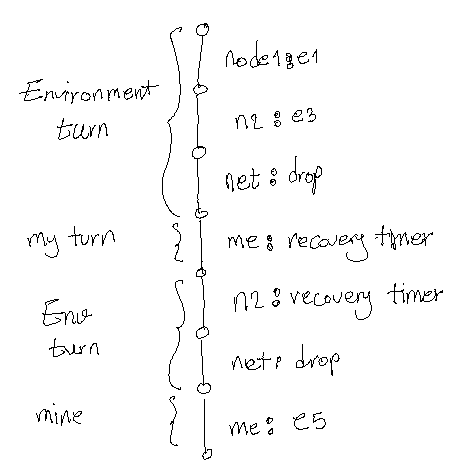We have 3 different type of events:

1. (COM) Communication Errors: drop pkt, TCP rst, node reset.
2. (USR) User Triggers: Application events like join overlay
3. (PRTCL) Protocol designed events: like receiving a sent message to us, running an expired scheduler, …

This is how we define the probabilities for this events

1. For COM events, we assign probabilities according to communication system statistics, like drop rate and so on.
2. For USR events, we assign probabilities according to application statistics.
3. For PRTCL events, we need to take the real time into consideration; For each event, we consider the time that it take for the event to occur and then we make the global time to go forward by that amount of time.
   • Messages: the times equals to average delay
   • Timers: It is almost zero, but we can consider the negligible handler running time here.

• Now that we have global time, we can define the probability of en event by this:
  • Probability(MSG) = exp(CURRENT TIME - MSG RECV TIME); for: MSG RECV TIME > CURRENT TIME
  • Probability(TIMER) = exp(CURRENT TIME - EXPIRATION TIME); for: EXPIRATION TIME > CURRENT TIME

The whole idea is depicted in this picture:

Note: We can extend this scheme by assigning min and max instead of absolute values for delays. One step further, we can define a general function for delays.

Cost function for each state can be something like this: where

• is the facet number i
  1. !safe →
  2. !live → transient time = time since state is not alive
  3. performance → e.g. tree balance
• is the weight of facet
• is the probability of entering to that state from current state.

We can look at the execution steering process as a two-player game: A node which is running the modelchecker and the whole environment which includes: other nodes events and communication events. As described in the picture below, it is not clear that how many steps environments plays.

We can look it as a Minimax game where I can not see the moves of my rival, i.e. I can not see what environment plays but I can see what I am playing.

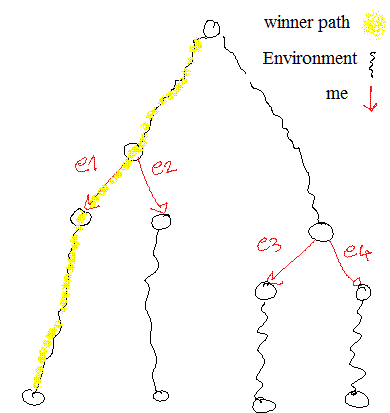
Winner path: The path which its values is selected as the finalist of minimax game.

Note: In our application one winner path is not enough. Because the absolute winner path may never happen in practice. Therefore, we should be ready for all possible plays of the environment.

The figure below describes it in more detail. Here, we have two different non-determinism point in our protocol {e1,e2} and {e3,e4}. Assume that the absolute winner path covers only {e1,e2}. Now, if in practice if the environment plays in a way that leads to {e3,e4}, then we do not know how to play because we do not know what path is the winner among the ones which covers {e3,e4} non-determinism.

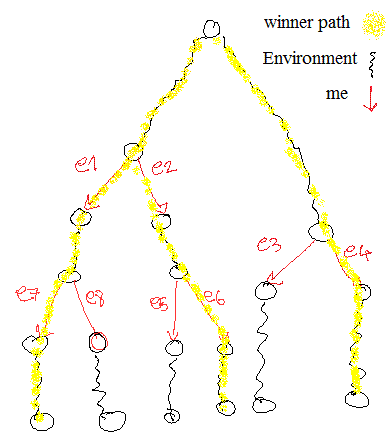
Furthermore, after our first play, we do not know what would be the reaction of the environment. In other words, I need to be prepared for all the possible non-determinism points for the next move as well. For example, In the above example assume that after non-determinism point {e1,e2} I might face {e5,e6} OR {e7,e8}. So, I need to memorize each of them as winner path as well. This is depicted in picture below.

Note: generally after my first move I can start the search again and we do not need to memorize a separate winner path for each of my next moves, but for the sake of efficiency, because I do not how much time I have to play my next move, it is better to take the next moves into consideration as well. It might also has a drawback of making alpha-beta pruning inefficient

The algorithm maintains two values, alpha and beta, which represent the minimum score that the maximizing player is assured of and the maximum score that the minimizing player is assured of respectively. Initially alpha is negative infinity and beta is positive infinity. As the recursion progresses the “window” becomes smaller. When beta becomes less than alpha, it means that the current position cannot be the result of best play by both players and hence need not be explored further.

• My pseudo code is easier to understand
• In each step we take into consideration only β
• In each step we update the α because it is β for the next step
• If β≤α we loose anyway, the return value is not important then.
• In β≤α, the initial α sent from top-level is not important, we keep the same variable for simplicity

function alphabeta(node, depth, α, β)         
    (* β represents previous player best choice - doesn't want it if α would worsen it *)
    if node is a terminal node or depth = 0
        return the heuristic value of node
    foreach child of node
        α := max(α, -alphabeta(child, depth-1, -β, -α))     
        (* use symmetry, -β becomes subsequently pruned α *)
        if β≤α
            return +inf  (*I loose to β anyway*)           (* Beta cut-off *)
    return α

(* Initial call *)
alphabeta(origin, depth, -inf, +inf)

The code below does exactly the same thing but it is easier to understand, for our purpose I will adapt this code.

(* the minimax value of n, searched to depth d.
 * If the value is less than min, returns min.
 * If greater than max, returns max. *)
 fun minimax(n: node, d: int, min: int, max: int): int =
   if leaf(n) or depth=0 return evaluate(n)
   if n is a max node
      v := min
      for each child of n
         v' := minimax (child,d-1,v,max)
         if v' > v, v:= v'
         if v > max return max
      return v
   if n is a min node
      v := max
      for each child of n
         v' := minimax (child,d-1,min,v)
         if v' < v, v:= v'
         if v < min return min
      return v

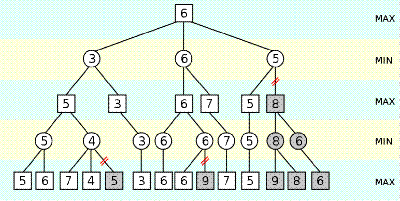
The figure below, describes the operation of alpha-beta pruning on a search tree.

• Do not prune along the path that I have not played at least once. This is to make sure that I am prepared to face all non-determinism points.
• Min and Max players do not necessarily switch their turn each time. In other words, Environment can play several moves at its turn.
• Moreover, at each step we may have possibility for both our moves and environment moves. Then
  1. We play min, like all the moves are for environment
  2. But, we keep track of my moves to be prepared in case
• We need to keep track of all winner paths, one for each of my non-determinism point.

(* the minimax value of n, searched to depth d.
 * If the value is less than min, returns min.
 * If greater than max, returns max. *)
 fun minimax(n: node, d: int, min: int, max: int): int =
   if leaf(n) or depth=0 return evaluate(n)
   if n is a max node
      v := min
      for each child of n
         v' := minimax (child,d-1,v,max)
         if v' > v, v:= v'
         if v > max return max
      return v
   if n is a min node
      v := max
      for each child of n
         v' := minimax (child,d-1,min,v)
         if v' < v, v:= v'
         if v < min return min
      return v