Of the use of cartesian products...
The purpose of this page is to summarize the current status of our plans on how to proceed with verification of PM expressions.
Using sets
Types
Sets are convenient to represent type. We will always consider a type T to be represented by the corresponding set  . Assume the following class hierarchy:
. Assume the following class hierarchy:
sealed abstract class Tree class Node(left: Tree, value: Int, right: Tree) extends Tree class Leaf() extends Tree
We would have the following properties on the corresponding sets:


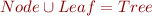
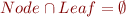
Extractors
Extractors are applied on types and return values for certain instances of these types. For a given extractor, we can define the set of values which it will match by an appropriate set. Note that it will of course be a subset of the matched type (note how we use type and set alternatively). For example, the following extractors:
object ENode { def unapply(node: Node): Option[(Tree,Int,Tree)] = Some(node.left, node.value, node.right) } object ELeaf { def unapply(leaf: Leaf): Boolean = true }
(alternatively, replace the boolean by Option[()] if you want)
…would have their corresponding sets:
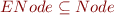
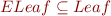
Now, a user could want to indicate that ENode not only matches Node's, but actually matches all of them (same for ELeaf of Leaf's). He would need to specify the following constraints:


(Note that we then have equality between the sets of the extractors and their corresponding types. This is the situation we have with case classes.)
Covering sets and disjoint extractors
Assume two new extractors:
object EvenNode { def unapply(node: Node) = if(node.value %2 == 0) Some(node.left, node.value, node.right) else None } object OddNode { def unapply(node: Node) = if(node.value %2 != 0) Some(node.left, node.value, node.right) else None }
We would like to indicate that:
- are disjoint: there exist no instance of Node that they both match
- form a cover: there exist no instance of Node which none of them matches
This is readily expressible thanks to the set operators:
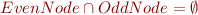

Analyzing patterns
Search space
In our approach, we represent the possible values for the scrutinee object as a tuple (a cartesian product of sets) representing the values the various encountered extractors can return when the scrutinee is tested against the patterns. The size and “type” of that tuple (i.e. the number of sets and which ones are used in the cartesian product) are determined by the patterns in the expression being analyzed.
The size is determined by the number of different positions where extractors are called. We define “different positions” by first defining “similar positions”. Two positions are similar if and only if it can be statically determined only by looking at the patterns that the set of objects which can be passed as parameter the extractor at these positions are the same. In other words, if you see patterns as trees, two positions are the same if and only if they are connected to the root by the exact same path. Note that:
- the number of different positions is trivially bounded by the number of calls to extractors
- there cannot be two similar positions in the same pattern
- we make no use of any knowledge about the behaviour of the extractors to determine the different positions
- all outer-most calls to extractors (the “root extractor” of the pattern) carry the same position, as any valid value for the scrutinee can be tested against these extractors
The type associated to a position is the corresponding part of the return tuple-type of the extractor where its found. A special case is the “root position” (see remark above), whose type is quite logically the type of the scrutinee.
( seriously, this next paragraph could be reformulated)
A convenient way to proceed with the analysis is to assign identifiers to the various positions. Once all different positions
seriously, this next paragraph could be reformulated)
A convenient way to proceed with the analysis is to assign identifiers to the various positions. Once all different positions 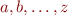 and their corresponding types
and their corresponding types 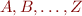 are identified, we can define the cartesian product
are identified, we can define the cartesian product 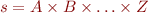 which somehow represents “the set of sets of values which can be submitted at the same time to the extractors of some pattern”. It is not unnatural to think of this as “everything which can be fed to the PM expression”, which is why we use the letter
which somehow represents “the set of sets of values which can be submitted at the same time to the extractors of some pattern”. It is not unnatural to think of this as “everything which can be fed to the PM expression”, which is why we use the letter  for scrutinee.
for scrutinee.
Note that this set is too large, since certain combinations don't make sense in terms of the patterns found in the PM expression, as typically not every pattern will contain an instance of each different positions, but this is not a concern.
Patterns
The set of values for the scrutinee which will be matched by a given pattern can now be seen as a subset of  expressed by constraints. Recall that each extractor
expressed by constraints. Recall that each extractor  has a corresponding set
has a corresponding set  which defines all values which it matches. A pattern will successfully match a value if all extractors in it match what they are submitted with. In other words, for a pattern with calls to extractors
which defines all values which it matches. A pattern will successfully match a value if all extractors in it match what they are submitted with. In other words, for a pattern with calls to extractors  is a cartesian product of the same dimension as
is a cartesian product of the same dimension as  , where the positions corresponding to the extractors are “replaced” with the proper sets:
, where the positions corresponding to the extractors are “replaced” with the proper sets:

. Note that by construction of the types 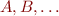 , this is always a subset of
, this is always a subset of  .
.
Completeness, disjointness and the like
As these expressions represent sets of values accepted by the patterns, disjointness, completeness, irredundancy and whatsoever are expressed straightforwardly by using 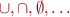 .
.
Examples
For the following examples, assume the usual binary tree representation and extractors.
Trivial
t: Tree match { case ENode(_,_,_) => ... case ELeaf() => ... }
There is only one position here, so we have 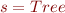 .
.
The constraints on the patterns are:
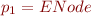
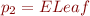
Completeness is expressed as  and disjointness as
and disjointness as 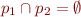 . Both are trivial with our axioms.
. Both are trivial with our axioms.
Less trivial
t: Tree match { case [a]EvenNode([b]OddNode(_,_,_),_,_) => ... case [a]EvenNode([b]EvenNode(_,_,_),_,_) => ... case [a]OddNode(_,_,_) => ... case [a]ELeaf() => ... }
Here we have two positions (“annoted” [a] and [b]). The types A and B are both Tree. We hence have  .
The constraints on the patterns are:
.
The constraints on the patterns are:


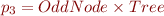

(recall that when a position is not present in a pattern we use its general type)
Ideas to follow
Complexity of the operations
We saw that the number of positions, hence the dimension of the sets we're operating with, is bounded by the number of extractor calls. An interesting remark is that the complexity of the verification operations (union for completeness or irredundancy, intersection and comparison to the empty set for disjointness) is not necessary directly proportional to that as well. Indeed, adding patterns without adding new extractors could actually make completeness easier to check (reaching the target set quicker with unions). Disjointness is in general quick to check, since it consists only in finding an axiom to apply in a list of the form 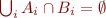 expressions (since disjointness of cartesian products can be reduced to that.
expressions (since disjointness of cartesian products can be reduced to that.
More can be read about this here.
Guards
Guards make things interesting. One idea we had was to incorporate the guards into the cartesian products. Indeed, the identifiers used in the operations can always be bound either to a method call (or field), which can be seen as a new position, or to part of the pattern, which will be then a position encountered already. This makes some things easy to check: for instance the pattern:
case ENode(_,i,_) if i > 2 => ...
…in a system with only two positions can be seen as the constraint:
![Equation \begin{equation*}p_i = ENode \times ]2;\infty[ \end{equation*}](/w/lib/exe/fetch.php?media=wiki:latex:/img9dd3b33f29bc72ffba0536d24716c9ec.png)
This works well for .isInstanceOf checks as well, but not for stuff like if i > j, as our cartesian products have no way to represent dependencies between members.
Guards, revisited
However, this is not how we finally decided to deal with guards. We opted for a two-step analysis.
For disjointness checks, we always test a pair of patterns. There are three possibilities:
- The patterns have no guard: Proceed as mentioned above.
- At least one of the patterns has a guard, and the patterns (without the guards) are different: ignore the guard(s) and proceed as usual.
- The patterns are identical, and only their guards
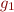 and
and  differ: check that
differ: check that 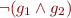 holds.
holds.
For completeness checks, we proceed slightly differently. When computing the union over the cartesian products, we take into account the product corresponding to a pattern p if and only if:
- Either p has no guard
- or p has a guard and we can find a set of patterns within the expression with the same signature such that the disjunction of their guards form the true statement
Both these approaches are conservative: they may prompt unnecessary warnings due to false negatives, but won't let any incomplete or non-disjoint expression go through unnoticed.
Nested patterns
Nested pattern matching seem to occur frequently enough in practice (at least in the world of case classes in Scala, possibly in OCaml as well) to give it a thought. The potential problem if we analyze nested pattern with taking only into consideration the type of the scrutinee, is that we miss a substantial part of the information about the shape of the scrutinee. Indeed, by the simple fact that it matched the pattern where it is nested is a crucial fact. Viktor gave the following example:
match t with | Leaf -> ... | Node(x,y) -> (match t with Node(u,v) -> ...)
The nested pattern match is complete because it happens inside the other case.
We can of course build even more complex examples where the complete structure of the “outer” pattern is required to determine completeness of the nested expression. Creativity finds no limit when we start writing patterns nested at the second, third, etc. level.
Using the current framework
The way we want to address this is as following. For starters, let's ignore guards. When analyzing the nested expression, we need at some point to count the different positions. We do this by considering the corresponding pattern (the one which leads to the nested expression) in the outer expression as well, as if it were part of the nested expression. Then, we generate the cartesian products as usual, but this time, when checking completeness, we use the cartesian product of the outside pattern as the set of possible values for the scrutinee. Intuitively, this really corresponds to the fact that we want to check completeness of the nested expression over the set of values matched by the outer pattern. (Note that in order to be able to do this, we cannot use the universal set to fill in the positions which don't appear in the outer pattern, but need to restrict ourselves to the most general type returned by the corresponding extractor.)
In the following example:
t: Tree match { case Node(Node(_,_,_), _, _) => t match { case Node(Node(Leaf,_,_),_,_) => ... case Node(Node(Node(_,_,_),_,_),_,_) => ... case WayTooComplexExtractor(FirstPart(_), SecondPart(_), YetAnotherPart(_,_,_)) => ... case Leaf() => ... }
We would build the two sets:
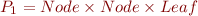 and
and
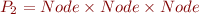 for the patterns of the nested expression,
for the patterns of the nested expression,
and the set
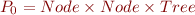 for the outer pattern.
for the outer pattern.
Checking completeness is then done by verifying that 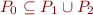 holds (which is the case), while checking disjointness is done as before.
holds (which is the case), while checking disjointness is done as before.
This approach works for expressions which use more and less restrictive patterns alike. We can also generalize the approach to expressions nested more deeply: when computing the cartesian products, we take into account all the patterns which had to be followed to reach the expression we're analyzing, then we use the intersection of the ones which are not part of that expression as the set of values for the scrutinee.
In "if" expressions
So far, our only plan for “if” expressions is to use whatever information we find about the type of the scrutinee as an axiom for the analysis.