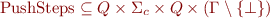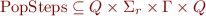This is an old revision of the document!
Visibly pushdown languages
What if a property that we wish to check is not regular?
Note that checking inclusion, emptyness of intersection, and universality of context-free languages are all undecidable. So we cannot check (without approximation) whether a pushdown system satisfies a context-free property. This is unfortunate, as some properties are context-free. There is a class of languages that are between regular and context-free and that have good closure properties. These can be used to check some properties that cannot be checked using the first approach.
Visibly pushdown languages are defined with respect to a pushdown alphabet, which is a triple 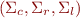 . Here
. Here
 is the set of calls (which will lead to push on a stack)
is the set of calls (which will lead to push on a stack) is the set of returns (which will lead to pop on a stack)
is the set of returns (which will lead to pop on a stack) is the set of local actions (which leave stack the same)
is the set of local actions (which leave stack the same)
Visibly pushdown automaton
A (nondeterministic) visibly pushdown automaton (on finite words) over the pushdown alphabet  is a tuple
is a tuple 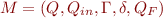 where
where
 is a finite set of states
is a finite set of states
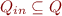 is the set of initial states
is the set of initial states
 is the set of final states
is the set of final states
 is a finite stack alphabet containing a special symbol
is a finite stack alphabet containing a special symbol 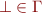
 where
where
Stack always contains  as the bottom element. A visibly pushdown automaton never pushes or pops
as the bottom element. A visibly pushdown automaton never pushes or pops  .
.
Closure properties
Determinization of visibly pushdown automaton
Note
- cannot store set of stacks (not a stack)
- if attempt to store stack of sets of symbols, lose connection between states and stacks
Solution: not just a set of states, but a summary of relation from initial to final states of 'procedure'. Then update directly the effect of a procedure call on each state.
Note: you never store original symbols on the stack.
References
- Rajeev Alur, P. Madhusudan: Visibly pushdown languages