This is an old revision of the document!
Simple QE for Dense Linear Orders
Example of dense linear order: rational numbers with less-than relation. (It works in the same way for real numbers with less-than relation.)
Theory of Dense Linear Orders
Language 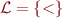 . Atomic formulas are of two forms:
. Atomic formulas are of two forms:
Literals are either atomic formulas or their negations.
Formulas  are the formulas that are closed formulas that are true in the structure
are the formulas that are closed formulas that are true in the structure 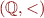 or rational numbers.
or rational numbers.
Example: The 'successor' formula: \[
\forall x. \exists y.\ x < y \ \land\ (\forall z. (x < z \rightarrow z=y \lor y < z)
\] Is this formula true in dense linear orders? Is there a non-dense linear order where its truth value is different?
Normal form of Formulas
We have seen that it suffices to eliminate quantifiers from conjunctions of literals.
Can we assume that literals are of a special form?
Example: simplify these formulas:
If we have three concrete values for 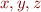 , what is the form of the strongest type of a formula that we could write about them in this language? (atomic type formula)
, what is the form of the strongest type of a formula that we could write about them in this language? (atomic type formula)
Theorem: every quantifier-free formula in a language with only relational symbols is a disjunction of atomic type formulas
- if we know the set
 of axioms, we may be able to show that the atomic type formulas have a simple form
of axioms, we may be able to show that the atomic type formulas have a simple form
Quantifier Elimination Step
Quantifier elimination from atomic type formulas:
Quantifier elimination from more general formulas:
Example: Use quantifier elimination to compute the truth value in dense linear orders for the example 'successor' formula above.



