This is an old revision of the document!

Simple QE for Dense Linear Orders

Example of dense linear order: rational numbers with less-than relation. (It works in the same way for real numbers with less-than relation.)

Theory of Dense Linear Orders

Language 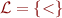${\cal L} = \{ < \}$ . Atomic formulas are of two forms:

Literals are either atomic formulas or their negations.

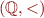Formulas $T$ are the formulas that are closed formulas that are true in the structure $(\mathbb{Q},<)$ or rational numbers.

We have seen that it suffices to eliminate quantifiers from conjunctions of literals.

Can we assume that literals are of a special form?

Example: simplify the formula \[

 x < y\ \land\ \lnot (y < z) \ \land\ (x \neq z)