This is an old revision of the document!

QBF and Quantifier Elimination

Quantified Propositional Formula Syntax

Eliminating quantifiers by expansion

We can apply the following rules to eliminate propositional quantifiers: \[

  \exists p. F \ \leadsto subst(\{p \mapsto {\it false}\},F) \lor subst(\{p \mapsto {\it true}\},F)

\] \[

  \forall p. F \ \leadsto subst(\{p \mapsto {\it false}\},F) \land subst(\{p \mapsto {\it true}\},F)

\] Note that the expansion can produce exponentially larger formula.

Notion of quantifier elimination applies to other logic as well.

Definition: A logic has quantifier elimination if for every formula in the logic, there exists an equivalent formula without quantifiers.

Definition: A quantifier elimination algorithm is an algorithm that takes a formula in a logic and converts it into an equivalent formula without quantifiers.

Note: Formula $F$ is valid iff $\forall p_1,\ldots,p_n. F$ is true.

Note: Formula $F$ is satisfiable iff 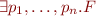$\exists p_1,\ldots,p_n. F$ is true.

In general QBF formulas can have alternations between $\forall$ and $\exists$ quantifiers: \[

 \forall p. \exists q. ((p \rightarrow q) \land (q \rightarrow r))

Notes on Computational Complexity

checking satisfiability of propositional formula $F$ is NP-complete
checking validity of propositional formula $F$ is coNP-complete
checking truth value of arbitrary QBF formula is PSPACE-complete