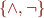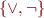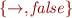This is an old revision of the document!
Normal Forms for Propositional Logic
Negation-Normal Form
In Negation-normal from, negations are only allowed on elementary proposition. Moreover, NNF formulas contain no implication, so the only binary operators are conjunctions and disjunctions. The following rules can be used to turn arbitrary propositional formulas into negation-normal form. \[\begin{array}{l}
\lnot (p \land q) \leftrightarrow (\lnot p) \lor (\lnot q) \\ p \leftrightarrow \lnot (\lnot p) \\ (p \rightarrow q) \leftrightarrow ((\lnot p) \lor q) \\ \lnot (p \lor q) \leftrightarrow (\lnot p) \land (\lnot q)
\end{array} \] Note that this transformation is linear in the size of the formula. No exponential blow-up.
Recall homework01.
Polarity of formula.
Disjunctive Normal Form
Formulas in Disjunctive-normal form look like this:

More formally 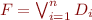 where
where  .
.
Each  is a clause and is defined as
is a clause and is defined as 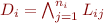 .
.
Each 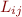 is a literal. It's either an elementary proposition or its negation.
is a literal. It's either an elementary proposition or its negation.
Solving the SAT problem for DNF formulas is in P, but transforming an arbitrary propositional formula to DNF causes an exponential blow-up.
DNF formulas can be easily generated from truth tables. Each row of the truth table that makes the formula true can be written as a clause. For a formula over  variables, there are
variables, there are  rows in the truth table. Over
rows in the truth table. Over  variables, there are
variables, there are 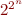 different (i.e. non-equivalent) formulas.
different (i.e. non-equivalent) formulas.
Conjunctive Normal Form
Formulas in Conjunctive-normal form look like this:

It's defined as 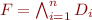 and
and 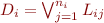
Like for DNF, 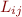 are elementary propositions or their negation. The terminology of clauses and literals also applies to CNF.
are elementary propositions or their negation. The terminology of clauses and literals also applies to CNF.
There is no polynomial-time equivalence preserving transformation to CNF or to DNF.
Complete Sets of Connectives
If we can express every formula. Examples:
 because every formula has DNF (or CNF)
because every formula has DNF (or CNF)
Circuits
Circuits (acyclic graph labelled by propositional operators) and formulas. if-then-else expression. Fresh variables.
Satisfiability-Preserving Transformation
Fresh variable idea: general technique for eliminating (or postponing) exponential blowup.
Satisfiability preserving transformation to CNF.
Flattening, expressing everything using  which in turn become clauses.
which in turn become clauses.
Optimization: for cases of only positive or only negative polarity.