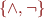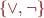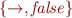LARA

This is an old revision of the document!

Normal Forms for Propositional Logic

Negation-Normal Form

Recall homework01.

Polarity of formula.

Size of NNF ?

Disjunctive Normal Form

Complete disjunctive normal form and truth tables.

  • generating DNF from truth table
  • generating DNF by transformations

Conjunctive Normal Form

CNF

Literal. Clause.

No polynomial-time equivalence preserving transformation to CNF or to DNF.

Complete Sets of Connectives

If we can express every formula. Examples:

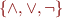  • $\{\land, \lor, \lnot\}$ because every formula has DNF (or CNF)
  • $\{\land,\lnot\}$
  • $\{\lor,\lnot\}$
  • $\{\rightarrow,{\it false}\}$
  • $\{\barwedge\}$
  • $\{\veebar\}$

Circuits

Circuits (acyclic graph labelled by propositional operators) and formulas. if-then-else expression. Fresh variables.

Satisfiability-Preserving Transformation

Fresh variable idea: general technique for eliminating (or postponing) exponential blowup.

Satisfiability preserving transformation to CNF.

Flattening, expressing everything using $\land, \lnot$ which in turn become clauses.

Optimization: for cases of only positive or only negative polarity.