This is an old revision of the document!
Homework 12, Due May 21
Problem 1
Write a regular expression in alphabet  denoting relation
denoting relation  using Regular expressions for automata with parallel inputs. Try to make your regular expression as concise and understandable as possible.
using Regular expressions for automata with parallel inputs. Try to make your regular expression as concise and understandable as possible.
Problem 2
Describe the set of all binary relations 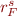 definable through singleton sets
\[
definable through singleton sets
\[
r^s_F = \{(p,q) \mid F(\{p\},\{q\}) \}
\]
where  are formulas of WS1S. How does this set of
are formulas of WS1S. How does this set of 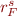 compare to the set of all binary relations definable in Presburger arithmetic
\[
compare to the set of all binary relations definable in Presburger arithmetic
\[
r^p_F = \{ (p,q) \mid G(p,q) \}
\]
where  is a Presburger arithmetic formula. Are the set of all
is a Presburger arithmetic formula. Are the set of all 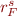 and set of all
and set of all 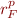 equal, is one strict subset, or are they incomparable?
equal, is one strict subset, or are they incomparable?
Optional Problem 3
In Quantifier elimination definition we noted that if the validity of first-order formulas in some theory is decidable, then we can extend the language of formulas so that we have quantifier elimination. Previously we also observed that quantifier elimination implies the existence of interpolants (see the definition of interpolation for propositional logic as well as the Calculus of Computation Textbook). We next apply these observations to weak monadic second-order logic over strings described in Lecture23.
Extend the language of monadic second-order logic over strings with new predicate symbols and describe an algorithm that, given formulas 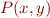 and
and 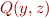 in this extension (where
in this extension (where  ,
, ,
, are
are  -tuples of set variables) checks whether
\[
-tuples of set variables) checks whether
\[
\forall x,y,z. (P(x,y) \rightarrow Q(y,z))
\]
holds, and, if it holds, finds an interpolant for 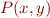 and
and 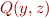 .
.