This is an old revision of the document!
Homework 07 - Due April 16
Problem 1
Select the topic of your project.
You may use current implementation homeworks as the starting point.
A list of possible project suggestions will appear here soon, but you are free to choose your own.
Submit a project proposal of length 200-1000 words. Summary project goal, why it is interesting, how you plan to solve it, and the difficulties you expect to encounter.
The proposal is not final, based on discussion with us you can reformulate the project.
Problem 2
Extend verification condition generator for integer programs from Problem 4 to handle procedures with supplied procedure specifications. Connect the verification condition generator to a theorem prover using the SMT-LIB interface. You may use this code: DecisionProc.scala, generously provided from by Damien from his previous homework. Your resulting program should be able to check whether program, defined as a collection of procedures manipulating integers, satisfies given preconditions and postconditions. For simplicity, you may assume that procedures do not return results and procedure calls are statements, not parts of expressions. There is no need to write a parser, use syntax trees, but do provide at least 3 test cases that illustrate the capabilities of the system.
Optional: insert checks that no result of arithmetic operation produces results whose absolute value is larger than 2^15-1.
Problem 3
Prove the following statement, which is a special case of a lemma used in quantifier elimination for set algebra.
Let 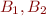 be two finite disjoint sets and
be two finite disjoint sets and 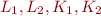 non-negative integers. Then the following two conditions are equivalent:
non-negative integers. Then the following two conditions are equivalent:
- there exists a finite set
 such that:
such that: 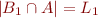 ,
, 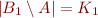 ,
, 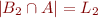 , and
, and 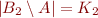 ;
; 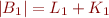 and
and 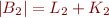 .
.