We will look at the languag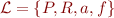e where

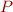• is relation symbol of arity one
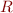• is relation symbol of arity two
• is a constant
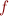• is a function symbol of two arguments

Consider this formula in : \[ \begin{array}{l@{}l}

& (\forall x. \exists y.\ R(x,y))\ \land \\
    & (\forall x. \forall y.\ R(x,y) \rightarrow \forall z.\ R(x,f(y,z)))\ \land \\
    & (\forall x.\ P(x) \lor P(f(x,a)))\ \\
    & \rightarrow \forall x. \exists y.\ R(x,y) \land P(y)

\end{array} \] We are interested in checking the validity of this formula (is it true in all interpretations). We will check the satisfiability of the negation of this formula (does it have a model): \[ \begin{array}{l@{}l} \lnot \bigg( \big( & (\forall x. \exists y.\ R(x,y))\ \land

    & (\forall x. \forall y.\ R(x,y) \rightarrow \forall z.\ R(x,f(y,z)))\ \land \\
    & (\forall x.\ P(x) \lor P(f(x,a)))\ \big)\\
    & \rightarrow \forall x. \exists y.\ R(x,y) \land P(y) \bigg)

\end{array} \]

Parsing the formula.

Negation normal form.

Skolem normal form for each clause.

Herbrand universe.

Propositional expansion.

Propositional proof.

Recovering first-order proof from propositional proof.