This is an old revision of the document!

Compactness for First-Order Logic

Theorem (Compactness for First-Order Logic): If every finite subset of a set 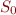$S_0$ of first-order formulas has a model, then 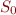$S_0$ has a model.

Proof:

Let 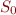$S_0$ be a set of first-order formulas.

Suppose 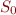$S_0$ has no model.

Then 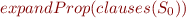$expandProp(clauses(S_0))$ has no model.

Some finite subset 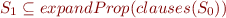$S_1 \subseteq expandProp(clauses(S_0))$ of it has no model.

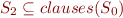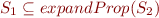There is then finite subset of clauses $S_2 \subseteq clauses(S_0)$ that generate $S_1$ , i.e. such that $S_1 \subseteq expandProp(S_2)$ . Therefore, $S_2$ has no model.

These clauses are generated by a finite subset 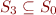$S_3 \subseteq S_0$ , i.e. $S_2 \subseteq clauses(S_3)$ .

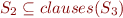Therefore 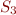$S_3$ has no model.

End of Proof.