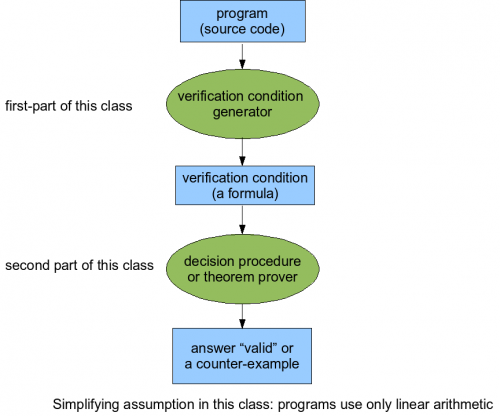
The structure of this lecture is similar to the previous one:

Today, we extend the approach from last lecture (both generating and proving formulas) to support data structures such as references and arrays.

We use weakest preconditions, although you could also use strongest postconditions or any other variants of the conversion from programs to formulas.

• what holds, why, and when

Can we derive wp(Q,havoc(x)?

• By consider havoc(x) as (… [] x=-1 [] x = 0 [] x = 1 [] …) ?
• From relational definition?

By wp semantics of havoc and assume

wp(Q, havoc(x); assume(x=t)) = 

while [inv I] (F) c1

⇒

assert(I);
havoc(x1,...,xn);    (those that can be modified in the loop)
assume(I);
assume(~F);

Provided that I is inductive. We can check that I is inductive by proving:

assume(I);
assume(F);
c1;
assert(I);

in isolation. Or proving

havoc(x1,...,xn)
assume(I);
assume(F);
c1;
assert(I);

at any point. If we combine these two, we get:

⇒

assert(I);
havoc(x1,...,xn);
assume(I);
 (assume(~F) []
  assume(F);
  c1;
  assert I;
  assume(false));

Benefit: if there is x_{n+1} that is not changed, we do not need to write its properties in the loop invariant. This can make loop invariant shorter.

If then else expressions.

Desugaring if-then-else.

Avoiding exponential explosion using flattening.

Array bounds checking.

Objects as references, null as an object.

Null checks.

All objects exist.

The allocated object set.

Why we need so many arguments.

Again, the second part! More technical. But, often you can use these things as a black box.

Properties of relations

• equivalence relation
• congruence; example from modular arithmetic

Equality is a congruence with respect to all function symbols.

Consider quantifier-free formulas with both linear arithmetic and uninterpreted functions.

• disjunctive normal form
• flatten
• separate
• check satisfiability separately

The harder part: proving that it is complete.

Using a SAT solver to enumerate disjunctive normal form disjuncts.

Standard for satisfiability checking of formulas, competition: http://combination.cs.uiowa.edu/smtlib

Note: we can also encode entire formula into SAT.

Notion of formal proof.

Minimality and independence of axioms - not so important for us.

Proof rules for first-order logic.

• propositional axioms
• instantiation
• generalization

Example: axiomatizing some set operations.

Two different techniques (recall we can take negation of formulas):

• Enumerating finite models (last time) gives us a way to show formula is satisfiable
• Enumerating proofs gives us a way to show that formula is valid

The gap in the middle: invalid formulas with only infinite models

• an example with only infinite models: strict partial order with no upper bound

From formulas to clauses

• negation normal form
• prenex form
• Skolemization
• conjunctive normal form

Unification.

Resolution and factoring proof rules.

Theorem prover competition: http://www.cs.miami.edu/~tptp/