This is an old revision of the document!
Reachable pushdown configurations are regular
We next show that in a push down system, the pre-image of a regular set of configurations is again a regular set of configurations. Moreover, the new finite state machine for configurations can use the same set of states as the original one. This gives an algorithm for verifying regular properties of push down automata by representing them using finite state machines. Based on the introductory part of Reachability Analysis of Pushdown Automata: Application to Model Checking.
Pushdown system
A pushdown system is a triple 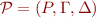 where
where
 is a finite set of states, called control locations
is a finite set of states, called control locations is a finite stack alphabet
is a finite stack alphabet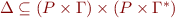 is a set of transition rules
is a set of transition rules
This is like a pushdown automaton, but there are no input symbols, and there are no final states. This is because we are interested in reachable states, not the language accepted by the automaton. If 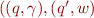 , we write
, we write  . Intuitively, this condition means that when the topmost stack symbol is
. Intuitively, this condition means that when the topmost stack symbol is  and the automaton is in the state
and the automaton is in the state  , the automaton can transition to a new state
, the automaton can transition to a new state  and replace the symbol
and replace the symbol  with the string
with the string  . Note that, as a special case, if
. Note that, as a special case, if  is an empty string, the automaton does a pop, and if the string is of the form
is an empty string, the automaton does a pop, and if the string is of the form  , then it pushes
, then it pushes  on top of the stack.
on top of the stack.
The configuration of a pushdown system is given by a pair 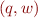 where
where  and
and  . The transition relation on configurations is given by relation
. The transition relation on configurations is given by relation
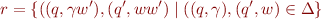
In an application to verification, this relation represents the meaning of the program. We are therefore interested in propagating error states backwards from some set of states to determine all initial states that could lead to an error.