LARA

• We say that two patterns have the same signature if, without their (optional) guard, they are identical.
• The set of pattern is assumed to be the cartesian product representing the set of inputs that a pattern would match.

The maximum number of different positions 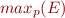which can be found in a given pattern matching expression is naturally linear in terms of the size of the source code (whether you want to measure this as tokens, elements of the AST or characters is irrelevant).

…in terms of the size of the source code, that is. This should be obvious…

We know that to every pattern corresponds one cartesian product. By construction, the dimension of these products is always the same since it corresponds to 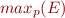. In particular, this means that taking the union of two “pattern sets” will yield yet another cartesian product with the same cardinality.

Note that we now also have:

\[ (A_1 \times A_2 \times \ldots \times A_n) \cap (B_1 \times B_2 \times \ldots \times B_n) = \emptyset \iff (A_1 \cap B_1 = \emptyset ) \vee (A_2 \cap B_2 = \emptyset ) \vee \ldots \vee (A_n \cap B_n = \emptyset ) \]

The proof is straightforward, but still requires that the dimensions match, otherwise the intersection could be empty for this other reason.

Recall that disjunction is verified for each pair of patterns. There are two options:

1. Either the patterns have different signatures, in which case we ignore their guards and verify that the interesection of their sets is empty…
2. …or they have the same signature, in which case we simply verify that the conjunction of their guards is false.

Since we limit our boolean expressions to QFBAPA ( do we?)