Invariant Inference Perspective
Strongest and weakest invariant,  , to prove that the program
, to prove that the program
s1; r*; s3
when started in a state from set  ends with a state from
ends with a state from  .
.
Take 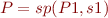 ,
, 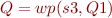 .
.
Hint: consider 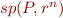 and
and 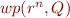 .
.
Find the strongest, weakest, and a simple invariant for the Hoare triple:
assume(x > 5 && y == 0)
while (x > 0) {
y = y + x
x = x - 1
}
assert(y > 5)
So, we can go from beginning or from the end.
Or we can go faster than sp, using some 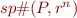 . This ensures we are above
. This ensures we are above 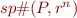 and then we check if we managed to prove the assertion.
and then we check if we managed to prove the assertion.
Dually, we could start from some stronger 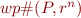 and check if we can ensure with the precondition.
and check if we can ensure with the precondition.
To formalize working with  and
and 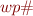 we use monotone functions on lattices.
we use monotone functions on lattices.
Exercise
Let  be a set (e.g. the set of all integers). Let
be a set (e.g. the set of all integers). Let  and
and 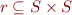 . Define
. Define

For each element 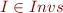 we have
we have 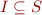 and we think of
and we think of  as an invariant. Assume
as an invariant. Assume 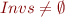 .
.
a): Show 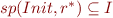 and
and
 for each
for each 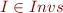 .
.
b) Show that 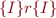 iff
iff 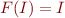 where
where  is a function from sets of states to sets of states,
is a function from sets of states to sets of states,  defined by
defined by
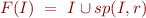
Moreover, 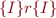 iff
iff 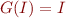 for
for
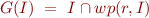
c): If  , is
, is  ?
?
d): If  , is
, is  ?
?
e): Let  and let
and let

in other words, by definition of  ,
,
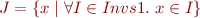
Prove that then 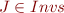 .
.
- What do we obtain for
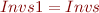 ?
?