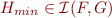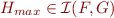Applications of Quantifier Elimination
Quantifier elimination works by eliminating quantifiers and produces an equivalent formula.
Example: By eliminating quantifier over  from the formula
from the formula
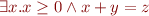
we obtain formula

Example: By eliminating all quantifiers from the formula
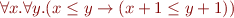
we obtain the formula 'true'.
Example: By eliminating quantifier  from the formula
from the formula
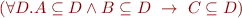
we obtain formula
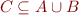
We review several uses of quantifier elimination.
Deciding Formula Validity and Satisfiability using Quantifier Elimination
Quantified formulas:
- eliminate quantifiers
- obtain ground formula
- evaluate ground formula
Satisfiability:
- add existential quantifiers
- check the resulting quantified formula
Validity:
- Check satisfiability of negation
Often we have better algorithms for quantifier-free fragments.
In such cases, we stop when we obtain formulas that has only existential quantifiers.
- for quantified formula the goal becomes to remove all quantifiers except for innermost existential quantifiers
The Purpose of Quantifiers
Suppose we want to describe a set of states of an integer program manipulating varibles  . We describe it by a formula
. We describe it by a formula 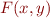 in theory admitting QE.
in theory admitting QE.
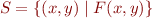
Then there is equivalent formula 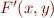 that contains no quantifiers, so it defines same set of states:
that contains no quantifiers, so it defines same set of states:
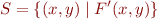
Are quantifiers useful when there is qe?
- to an extent, qe does show quantifiers are not necessary
 can be (more than) exponentially larger than
can be (more than) exponentially larger than 
- sometimes quantifiers naturally come up when encoding the problem
Quantifier Elimination in Relation Composition
What class of relations is defined by integer programs without loops in the syntax of Simple Programming Language ?
The class given by formulas in Presburger arithmetic.
Assignment:
Havoc:
Assume:
Non-deterministic choice:
Relation composition:
What does quantifier elimination tell us about representations of such formulas?
Quantifier Elimination for Optimization
We considered validity and satisfiability problems, which produce solutions or proofs.
Optimization problems try to find a maximum or minimum of some function, subject to given constraints.
problem 1 in this homework shows how to (in principle) use quantifier elimination for optimization.
Example reference:
Interpolation
Definition of Interpolant:
Given two formulas  and
and  , such that
, such that 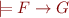 , an interpolant for
, an interpolant for 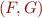 is a formula
is a formula  such that:
such that:
1) 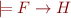
2) 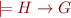
3) 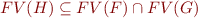
Paper on Interpolation in Verification
Here are two simple ways to construct an interpolant:
- We can quantify existentially all variables in
 that are not in
that are not in  .
.
 where
where 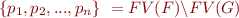
- We can quantify universally all variables in
 that are not in
that are not in  .
.
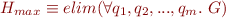 where
where 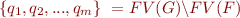
Definition: 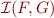 denote the set of all interpolants for
denote the set of all interpolants for 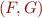 , that is,
, that is,

Theorem: The following properties hold for  ,
,  ,
, 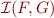 defined above:
defined above:
We have observed before that, if a theory has quantifier elimination, then it also has interpolants.
Therefore, all theories in the List of Theories Admitting QE have interpolants. (But interpolants may exist even if there is no quantifier elimination.)